题目内容
已知向量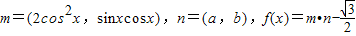 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线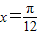 对称,且
对称,且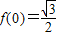
(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)函数的图象经过怎样平移变换能使所得图象对应的函数为偶函数?
【答案】分析:先求出f(x)的解析式,再根据正弦型函数的性质进行求解,具体是:先把函数式化成形如y=Asin(ωx+φ)(ω>0)的形式,(1)根据T= ,确定函数的同期;(2)再根据基本三角函数的单调区间,求出x所在的区间.(3)偶函数的图象关于原点对称,即当x=0时,函数取最值.
,确定函数的同期;(2)再根据基本三角函数的单调区间,求出x所在的区间.(3)偶函数的图象关于原点对称,即当x=0时,函数取最值.
解答:解:(1)f(x)=
=
∵且 ∴
∴
又∵函数f(x)的图象关于直线 对称
对称
∴f( )=f(0)∴b=1
)=f(0)∴b=1
∴f(x)=
∴T= =π
=π
(2)当f(x)单调递增时,
∴
∴f(x)的单调递增区间为
(3)f(x)=sin(2x+ )=cos2(x-
)=cos2(x- )
)
∴f(x)的图象向左平移 个单位后,所对应的函数为偶函数
个单位后,所对应的函数为偶函数
点评:在求正弦型函数的性质时,要遵循以下步骤:①先把函数式化成形如y=Asin(ωx+φ)(ω>0)的形式⇒②根据T= ,确定函数的同期⇒③再根据基本三角函数的单调区间,求出x所在的区间⇒④偶函数的图象关于原点对称,即当x=0时,函数取最值.
,确定函数的同期⇒③再根据基本三角函数的单调区间,求出x所在的区间⇒④偶函数的图象关于原点对称,即当x=0时,函数取最值.
 ,确定函数的同期;(2)再根据基本三角函数的单调区间,求出x所在的区间.(3)偶函数的图象关于原点对称,即当x=0时,函数取最值.
,确定函数的同期;(2)再根据基本三角函数的单调区间,求出x所在的区间.(3)偶函数的图象关于原点对称,即当x=0时,函数取最值.解答:解:(1)f(x)=

=

∵且
 ∴
∴
又∵函数f(x)的图象关于直线
 对称
对称∴f(
 )=f(0)∴b=1
)=f(0)∴b=1∴f(x)=

∴T=
 =π
=π(2)当f(x)单调递增时,

∴

∴f(x)的单调递增区间为

(3)f(x)=sin(2x+
 )=cos2(x-
)=cos2(x- )
)∴f(x)的图象向左平移
 个单位后,所对应的函数为偶函数
个单位后,所对应的函数为偶函数点评:在求正弦型函数的性质时,要遵循以下步骤:①先把函数式化成形如y=Asin(ωx+φ)(ω>0)的形式⇒②根据T=
 ,确定函数的同期⇒③再根据基本三角函数的单调区间,求出x所在的区间⇒④偶函数的图象关于原点对称,即当x=0时,函数取最值.
,确定函数的同期⇒③再根据基本三角函数的单调区间,求出x所在的区间⇒④偶函数的图象关于原点对称,即当x=0时,函数取最值. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
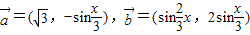 ,函数f(x)=
,函数f(x)=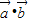 .
. 且
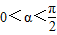
且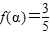 ,求
,求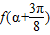 的值.
的值.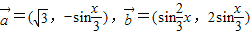 ,函数f(x)=
,函数f(x)=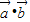 .
. 且
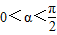
且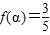 ,求
,求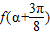 的值.
的值.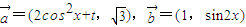 ,函数f(x)=
,函数f(x)=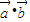 .
.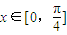 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.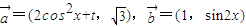 ,函数f(x)=
,函数f(x)=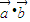 .
.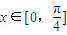 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.