题目内容
已知向量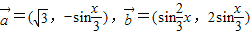 ,函数f(x)=
,函数f(x)=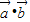 .
.(1)求f(x)的对称轴方程;
(2)若
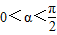 且
且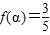 ,求
,求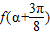 的值.
的值.
【答案】分析:(1)由题意可得函数f(x)的解析式,由整体法可得对称轴;
(2)由(1)可得sin( )=
)= ,进而可得cos(
,进而可得cos( ),而
),而 =2sin(
=2sin(
 )-1=2sin[(
)-1=2sin[( )+
)+ ]-1,由两角和与差的公式可得答案.
]-1,由两角和与差的公式可得答案.
解答:解:(1)由题意可得:函数f(x)= =
=
= =2sin(
=2sin( )-1,
)-1,
由 =kπ+
=kπ+ ,k∈Z可得x=
,k∈Z可得x= kπ+
kπ+ .
.
故f(x)的对称轴方程为:x= kπ+
kπ+ ,k∈Z
,k∈Z
(2)由(1)知:2sin( )-1=
)-1= ,解得sin(
,解得sin( )=
)= ,
,
结合 可得cos(
可得cos( )=
)= .
.
而 =2sin(
=2sin(
 )-1=2sin[(
)-1=2sin[( )+
)+ ]-1
]-1
=2sin( )cos
)cos +2cos(
+2cos( )sin
)sin -1
-1
=2× ×
×
 -1
-1
=
点评:本题为三角函数和向量的数量积的结合,两角和与差的三角函数公式是解决问题的关键,属中档题.
(2)由(1)可得sin(
 )=
)= ,进而可得cos(
,进而可得cos( ),而
),而 =2sin(
=2sin(
 )-1=2sin[(
)-1=2sin[( )+
)+ ]-1,由两角和与差的公式可得答案.
]-1,由两角和与差的公式可得答案.解答:解:(1)由题意可得:函数f(x)=
 =
=
=
 =2sin(
=2sin( )-1,
)-1,由
 =kπ+
=kπ+ ,k∈Z可得x=
,k∈Z可得x= kπ+
kπ+ .
.故f(x)的对称轴方程为:x=
 kπ+
kπ+ ,k∈Z
,k∈Z(2)由(1)知:2sin(
 )-1=
)-1= ,解得sin(
,解得sin( )=
)= ,
,结合
 可得cos(
可得cos( )=
)= .
.而
 =2sin(
=2sin(
 )-1=2sin[(
)-1=2sin[( )+
)+ ]-1
]-1=2sin(
 )cos
)cos +2cos(
+2cos( )sin
)sin -1
-1=2×
 ×
×
 -1
-1=

点评:本题为三角函数和向量的数量积的结合,两角和与差的三角函数公式是解决问题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
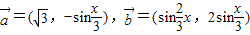 ,函数f(x)=
,函数f(x)=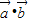 .
.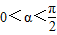 且
且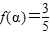 ,求
,求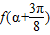 的值.
的值.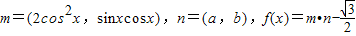 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线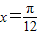 对称,且
对称,且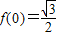
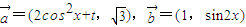 ,函数f(x)=
,函数f(x)=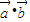 .
.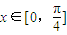 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.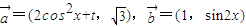 ,函数f(x)=
,函数f(x)=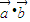 .
.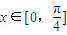 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.