题目内容
已知直线l的极坐标方程是ρsin(θ+| π |
| 3 |
| x2 |
| a2 |
| y2 |
| 6 |
分析:先将直线l的极坐标方程化成直角坐标方程,再求出双曲线的一条渐近线,最后利用平行线的斜率相等即可求得实数a值.
解答:解:直线l的极坐标方程是ρsin(θ+
)=1,
得其直角坐标方程为:
x+y-2=0,
又双曲线
-
=1(a>0)的一条渐近线是:
y=-
x,
∴
=
,a=
.
故答案为:
.
| π |
| 3 |
得其直角坐标方程为:
| 3 |
又双曲线
| x2 |
| a2 |
| y2 |
| 6 |
y=-
| ||
| a |
∴
| ||
| a |
| 3 |
| 2 |
故答案为:
| 2 |
点评:本题考查点的极坐标和直角坐标的互化、简单曲线的极坐标方程、双曲线的简单性质、两条直线平行的判定,极坐标和直角坐标的互化主要是利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
相关题目
 =a,a∈R圆,C的参数方程是
=a,a∈R圆,C的参数方程是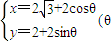 为参数),若圆C关于直线l对称,则a= .
为参数),若圆C关于直线l对称,则a= .