题目内容
(2013•湖南模拟)设极点与坐标原点重合,极轴与x轴正半轴重合,已知直线l的极坐标方程是:ρsin(θ-
)=a,a∈R圆,C的参数方程是
(θ为参数),若圆C关于直线l对称,则a=
| π |
| 3 |
|
-2
-2
.分析:将两曲线方程化为直角坐标方程,根据题意可得圆心在直线上,圆心的坐标适合直线的方程,由此求得实数a的取值.
解答:解:将两曲线方程化为直角坐标坐标方程,得直线l直角坐标方程为:
x-y+2a=0,
C:(x-2
)2+(y-2)2=4.
因为圆C关于直线l对称,所以,圆心在直线上,圆心的坐标适合直线的方程,
即
×2
-2+2a=0,
解得a=-2.
故答案为:-2.
| 3 |
C:(x-2
| 3 |
因为圆C关于直线l对称,所以,圆心在直线上,圆心的坐标适合直线的方程,
即
| 3 |
| 3 |
解得a=-2.
故答案为:-2.
点评:本题考查把极坐标方程化为直角坐标方程的方法,直线与圆的位置关系,属于基础题.

练习册系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=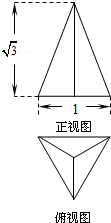 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )