题目内容
(本小题满分14分)设椭圆方程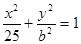 (
(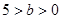 ),
),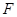 为椭圆右焦点,
为椭圆右焦点,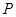 为椭圆在短轴上的一个顶点,
为椭圆在短轴上的一个顶点,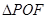 的面积为6,(
的面积为6,(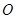 为坐标原点);
为坐标原点);
(1)求椭圆方程;
(2)在椭圆上是否存在一点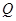 ,使
,使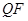 的中垂线过点
的中垂线过点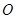 ?若存在,求出
?若存在,求出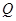 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
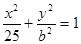 (
(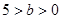 ),
),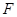 为椭圆右焦点,
为椭圆右焦点,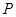 为椭圆在短轴上的一个顶点,
为椭圆在短轴上的一个顶点,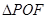 的面积为6,(
的面积为6,(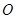 为坐标原点);
为坐标原点);(1)求椭圆方程;
(2)在椭圆上是否存在一点
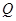 ,使
,使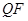 的中垂线过点
的中垂线过点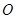 ?若存在,求出
?若存在,求出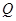 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.解:(1)设
∵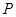 为椭圆在短轴上的一个顶点,且
为椭圆在短轴上的一个顶点,且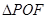 的面积为6,
的面积为6,
∴ . ----------------------------------------------------------- 1分
. ----------------------------------------------------------- 1分
又∵ ----------------------------------------------------------2分
----------------------------------------------------------2分
∴ 或
或 ---------------------------------------------------------4分
---------------------------------------------------------4分
∴椭圆方程为 或
或 ---------------------------------------6分
---------------------------------------6分
(2)假设存在点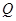 ,使
,使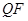 的中垂线过点
的中垂线过点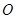 .
.
若椭圆方程为 ,则
,则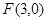 ,由题意,
,由题意,
∴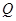 点的轨迹是以
点的轨迹是以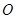 为圆心,以3为半径的圆.
为圆心,以3为半径的圆.
设 ,则其轨迹方程为
,则其轨迹方程为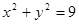 -------------------------------------------8分
-------------------------------------------8分
显然与椭圆 无交点.
无交点.
即假设不成立,点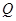 不存在. -----------------------------------------------9分
不存在. -----------------------------------------------9分
若椭圆方程为 ,
,
则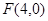 ,
,
∴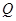 点的轨迹是以
点的轨迹是以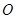 为圆心,以4为半径的圆.
为圆心,以4为半径的圆.
则其轨迹方程为 -----------------------------------------1 1分
-----------------------------------------1 1分
则 ,∴
,∴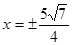 ,
,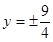 -------------------------------------------- 13分
-------------------------------------------- 13分
故满足题意的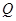 点坐标分别为
点坐标分别为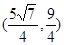 ,
, ,
, ,
,
---- 14分

∵
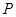 为椭圆在短轴上的一个顶点,且
为椭圆在短轴上的一个顶点,且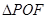 的面积为6,
的面积为6,∴
 . ----------------------------------------------------------- 1分
. ----------------------------------------------------------- 1分又∵
 ----------------------------------------------------------2分
----------------------------------------------------------2分∴
 或
或 ---------------------------------------------------------4分
---------------------------------------------------------4分∴椭圆方程为
 或
或 ---------------------------------------6分
---------------------------------------6分(2)假设存在点
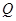 ,使
,使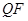 的中垂线过点
的中垂线过点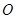 .
.若椭圆方程为
 ,则
,则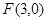 ,由题意,
,由题意,
∴
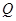 点的轨迹是以
点的轨迹是以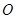 为圆心,以3为半径的圆.
为圆心,以3为半径的圆. 设
 ,则其轨迹方程为
,则其轨迹方程为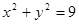 -------------------------------------------8分
-------------------------------------------8分显然与椭圆
 无交点.
无交点.即假设不成立,点
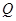 不存在. -----------------------------------------------9分
不存在. -----------------------------------------------9分若椭圆方程为
 ,
,则
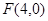 ,
,
∴
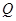 点的轨迹是以
点的轨迹是以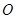 为圆心,以4为半径的圆.
为圆心,以4为半径的圆. 则其轨迹方程为
 -----------------------------------------1 1分
-----------------------------------------1 1分则
 ,∴
,∴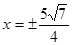 ,
,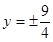 -------------------------------------------- 13分
-------------------------------------------- 13分故满足题意的
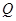 点坐标分别为
点坐标分别为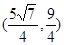 ,
, ,
, ,
,
---- 14分
略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
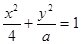 与双曲线
与双曲线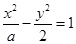 有相同的焦点,则
有相同的焦点,则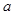 的值是
的值是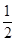
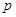 :方程
:方程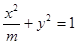 表示焦点在y轴上的椭圆; 命题
表示焦点在y轴上的椭圆; 命题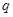 :直线
:直线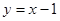
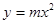 有两个交点
有两个交点 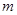 的取值范围
的取值范围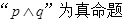 ,求实数
,求实数 的长轴长,短轴长,离心率依次是( )
的长轴长,短轴长,离心率依次是( )

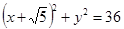 及定点
及定点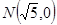 ,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足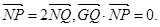
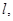 与曲线C交于A、B两点,O是坐标原点,设
与曲线C交于A、B两点,O是坐标原点,设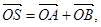 是否存在这样的直线
是否存在这样的直线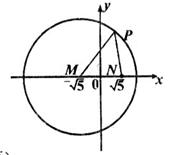

 的两焦点,
的两焦点, 是椭圆在第一象限弧上一点,且满足
是椭圆在第一象限弧上一点,且满足 =1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
=1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
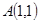 是椭圆
是椭圆 上一点,
上一点,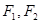 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足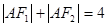
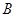 是椭圆上任意一点,如果
是椭圆上任意一点,如果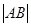 最大时,求证
最大时,求证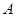 、
、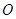 不对称.
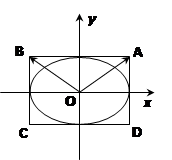
不对称.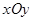 中,椭圆
中,椭圆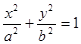 (
(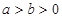 )被围于由
)被围于由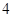 条直线
条直线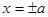 ,
,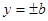 所围成的矩形
所围成的矩形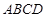 内,任取椭圆上一点
内,任取椭圆上一点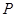 ,若
,若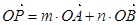 (
(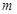 、
、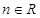 ),则
),则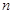 满足的一个等式是_______________.
满足的一个等式是_______________.