题目内容
.(本小题满分14分)
已知圆M: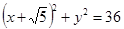 及定点
及定点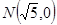 ,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足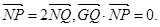
(1)求点G的轨迹C的方程;
(2)过点K(2,0)作直线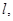 与曲线C交于A、B两点,O是坐标原点,设
与曲线C交于A、B两点,O是坐标原点,设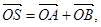 是否存在这样的直线
是否存在这样的直线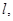 使四边形OASB的对角线相等?若存在,求出直线
使四边形OASB的对角线相等?若存在,求出直线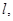 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
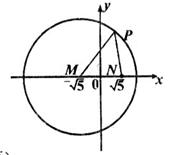
已知圆M:
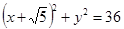 及定点
及定点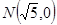 ,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足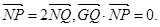
(1)求点G的轨迹C的方程;
(2)过点K(2,0)作直线
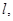 与曲线C交于A、B两点,O是坐标原点,设
与曲线C交于A、B两点,O是坐标原点,设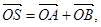 是否存在这样的直线
是否存在这样的直线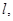 使四边形OASB的对角线相等?若存在,求出直线
使四边形OASB的对角线相等?若存在,求出直线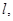 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1)由
 为PN的中点,且
为PN的中点,且 是PN的中垂线,
是PN的中垂线, ,
,∴>
 >
> ……………………(4分)
……………………(4分)∴点G的轨迹是以M、N为焦点的椭圆,又

∴
 ………………………………………………………………(6分)
………………………………………………………………(6分)(2)∵.
 四边形OASB为平行四边行,假设存在直线1,使
四边形OASB为平行四边行,假设存在直线1,使 四边形OASB为矩形
四边形OASB为矩形 若1的斜率不存在,则1的方程为
若1的斜率不存在,则1的方程为
由
 >0.这与
>0.这与 相矛盾,
相矛盾,∴1的斜率存在.……………………………………………………………………(8分)
设直线1的方程

|


 ∴
∴ …………………………………………(10分)
…………………………………………(10分)∴

由
 ∴
∴ …(13分)
…(13分)∴存在直线1:
 或
或 满足条件.…………………(14分)
满足条件.…………………(14分)略

练习册系列答案
相关题目
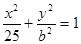 (
(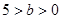 ),
),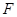 为椭圆右焦点,
为椭圆右焦点,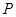 为椭圆在短轴上的一个顶点,
为椭圆在短轴上的一个顶点,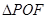 的面积为6,(
的面积为6,(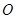 为坐标原点);
为坐标原点);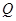 ,使
,使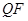 的中垂线过点
的中垂线过点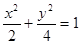 两焦点分别为F1、F2、P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2、P是椭圆在第一象限弧上一点,并满足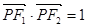 ,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点
,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点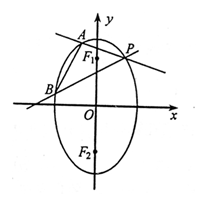
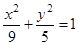 的中心和左焦点,点P为椭圆上任意一点,则
的中心和左焦点,点P为椭圆上任意一点,则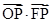 的最小值为
的最小值为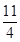
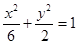 和双曲线
和双曲线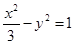 有公共焦点为
有公共焦点为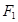 、
、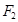 ,
,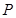 是两曲线的一个公共点,则
是两曲线的一个公共点,则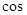 ∠
∠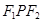 ( )
( )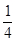

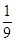

 的焦距为 ( )
的焦距为 ( )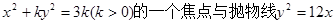 的焦点重合,则该椭圆的离心率是 .
的焦点重合,则该椭圆的离心率是 . ,过点
,过点 作倾斜角为
作倾斜角为 的直线
的直线 交椭圆于
交椭圆于 、
、 两点,
两点, 为坐标原点,则
为坐标原点,则 的面积为_____________.
的面积为_____________.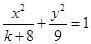 的离心率为
的离心率为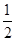 ,则
,则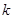 的值为 ____________
的值为 ____________