题目内容
已知PA⊥平面ABCD.ABCD为矩形AB=a,BC=2.Q为BC上一点.求a为何值时PQ⊥QD?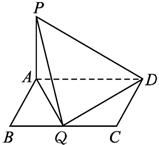
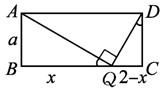
解：设BQ=x,则QC=2-x,连结AQ.
∵PA⊥面ABCD，要使PQ⊥QD，
只要AQ⊥QD即可.
由△ABQ∽△CDQ得
=
,∴x2-2x+a2=0,
Δ=4-4a2≥0,∴0＜a≤1.
故a∈(0,1］时,PQ⊥QD.
练习册系列答案
相关题目
题目内容
已知PA⊥平面ABCD.ABCD为矩形AB=a,BC=2.Q为BC上一点.求a为何值时PQ⊥QD?
解：设BQ=x,则QC=2-x,连结AQ.
∵PA⊥面ABCD，要使PQ⊥QD，
只要AQ⊥QD即可.
由△ABQ∽△CDQ得
=,∴x2-2x+a2=0,
Δ=4-4a2≥0,∴0＜a≤1.
故a∈(0,1］时,PQ⊥QD.
如图，三棱锥P-ABC中，已知PA⊥平面ABC，PA=3，PB=PC=BC=6，求二面角P-BC-A的正弦值．
（2012•宝鸡模拟）如图，已知PA⊥平面ABC，且
（2012•徐汇区一模）如图，已知PA⊥平面ABC，AC⊥AB，AP=BC=2，∠CBA=30°，D，E分别是BC，AP的中点．
（2012•徐汇区一模）如图，已知PA⊥平面ABC，AC⊥AB，AP=BC=2，∠CBA=30°，D是AB的中点．
（2013•盐城三模）如图，三棱锥P-ABC中，已知PA⊥平面ABC，△ABC是边长为2的正三角形，D，E分别为PB，PC中点．