题目内容
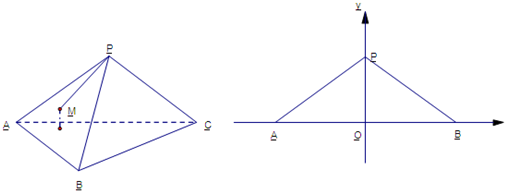
已知正三棱锥P-ABC中,点P,A,B,C都在半径为
的球面上,若PA,PB,PC两两互相垂直,则三棱锥P-ABC的体积为( )
| 3 |
分析:先将PA、PB、PC可看作是正方体的一个顶点发出的三条棱,所以过空间四个点P、A、B、C的球面即为的正方体的外接球,球的直径即是正方体的对角线,根据球的半径求出对角线长,进而得出正三棱锥P-ABC的侧棱长,从而求出三棱锥P-ABC的体积.
解答:解:∵空间四个点P、A、B、C在同一球面上,PA、PB、PC两两垂直,
则PA、PB、PC可看作是正方体的一个顶点发出的三条棱,
所以过空间四个点P、A、B、C的球面即为的正方体的外接球,球的直径即是正方体的对角线,
设PA=PB=PC=a,
∴
a=2
,∴a=2,
则三棱锥P-ABC的体积为
a3=
故选C.
则PA、PB、PC可看作是正方体的一个顶点发出的三条棱,
所以过空间四个点P、A、B、C的球面即为的正方体的外接球,球的直径即是正方体的对角线,
设PA=PB=PC=a,
∴
| 3 |
| 3 |
则三棱锥P-ABC的体积为
| 1 |
| 6 |
| 4 |
| 3 |
故选C.
点评:本题是基础题,考查球的内接体知识,考查空间想象能力,计算能力,分析出,正方体的对角线就是球的直径是解好本题的关键所在.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
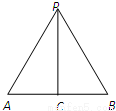
 已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为
已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为