题目内容
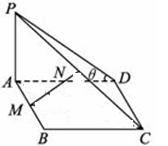
(1)求证:MN⊥AB;
(2)若平面PDC与平面ABCD所成的二面角为θ,能否确定θ的值,使得MN是异面直线AB与PC的公垂线?
(1)证明:连结AC,取AC中点Q,连结MQ、NQ,则NQ∥PA.
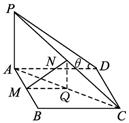
∵PA⊥平面ABCD,
∴NQ⊥平面ABCD.
∴NQ⊥AB.
又AB⊥MQ,
∴AB⊥平面MNQ.
∴AB⊥MN.
(2)解:∵AD⊥DC,PA⊥AD,∴∠PDA=θ.
若MN为PC与AB的公垂线,
则MN⊥PC.又N为PC的中点,
∴PM=MC.
若设BC=a,CD=2b,则MC=![]() =PM,
=PM,
∴PA=![]() =a.
=a.
∵PA=a=AD,
∴θ=45°.
故当θ=45°时,可使得MN是异面直线AB与PC的公垂线.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2012•丹东模拟)如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
(2012•丹东模拟)如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1, (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点. (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.