题目内容
5.若曲线y=lnx+ax2(a为常数)不存在斜率为负数的切线,则实数a的取值范围是( )| A. | (-$\frac{1}{2}$,+∞) | B. | [-$\frac{1}{2}$,+∞) | C. | (0,+∞) | D. | [0,+∞) |
分析 令y′≥0在(0,+∞)上恒成立可得a$≥-\frac{1}{2{x}^{2}}$,根据右侧函数的值域即可得出a的范围.
解答 解:y′=$\frac{1}{x}$+2ax,x∈(0,+∞),
∵曲线y=lnx+ax2(a为常数)不存在斜率为负数的切线,
∴y′=$\frac{1}{x}+2ax$≥0在(0,+∞)上恒成立,
∴a≥-$\frac{1}{2{x}^{2}}$恒成立,x∈(0,+∞).
令f(x)=-$\frac{1}{2{x}^{2}}$,x∈(0,+∞),则f(x)在(0,+∞)上单调递增,
又f(x)=-$\frac{1}{2{x}^{2}}$<0,
∴a≥0.
故选D.
点评 本题考查了导数的几何意义,函数单调性与函数最值,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
16. 如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )
如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )
 如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )
如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )| A. | ($\frac{3}{4}$,$\frac{5}{4}$) | B. | ($\frac{2\sqrt{17}}{17}$,4) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{3}{2}$) | D. | ($\frac{3\sqrt{5}}{10}$,$\frac{5}{4}$) |
13.理科竞赛小组有9名女生、12名男生,从中随机抽取一个容量为7的样本进行分析.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
规定85分以上(包括85份)为优秀,从这7名同学中再抽取3名同学,记这3名同学中物理和化学成绩均为优秀的人数为X,求随机变量X的分布列和数学期望.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
| 化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
20.如图所示的程序框图描述的为辗转相除法,若输入m=5280,n=1595,则输出的m=( )
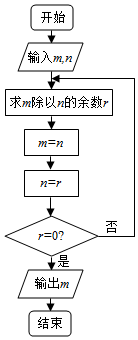

| A. | 2 | B. | 55 | C. | 110 | D. | 495 |
10.某项科研活动共进行了5次试验,其数据如表所示:
(Ⅰ)从5次特征量y的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(Ⅱ)求特征量y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并预测当特征量x为570时特征量y的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| 特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| x | 555 | 559 | 551 | 563 | 552 |
| y | 601 | 605 | 597 | 599 | 598 |
(Ⅱ)求特征量y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并预测当特征量x为570时特征量y的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
17.已知函数f(x)的定义域为R,当x∈[-2,2]时,f(x)单调递减,且函数f(x+2)为偶函数,则下列结论正确的是( )
| A. | f(π)<f(3)<f($\sqrt{2}$) | B. | f(π)<f($\sqrt{2}$)<f(3) | C. | f($\sqrt{2}$)<f(3)<f(π) | D. | f($\sqrt{2}$)<f(π)<f(3) |
14.三次函数f(x)=ax3-$\frac{3}{2}$x2+2x+1的图象在点(1,f(1))处的切线与x轴平行,则实数a=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
15.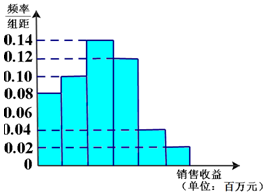 简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
(Ⅰ)根据频率分布直方图,计算图中各小长方形的宽度;
(Ⅱ)根据频率分布直方图,估计投入4万元广告费用之后,销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)按照类似的研究方法,测得另外一些数据,并整理得到下表:
表中的数据显示,x与y之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算y关于x的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
 简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片.当初向各地作了广告推广,同时广告对销售收益也有影响.在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.(Ⅰ)根据频率分布直方图,计算图中各小长方形的宽度;
(Ⅱ)根据频率分布直方图,估计投入4万元广告费用之后,销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)按照类似的研究方法,测得另外一些数据,并整理得到下表:
| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:百万元) | 2 | 3 | 2 | 7 |
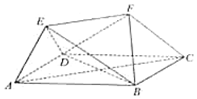 如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.