题目内容
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式及前
的通项公式及前![]() 项和
项和![]() ;
;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]()
![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() (2)
(2)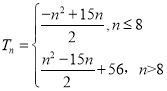 (3)
(3)![]()
【解析】
(1)设等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,由已知建立方程组
,由已知建立方程组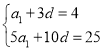 ,解之可得首项和公差,从而得出数列的通项和前n项和;
,解之可得首项和公差,从而得出数列的通项和前n项和;
(2)分当![]() 时和当
时和当![]() 时,分别求和可得数列
时,分别求和可得数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)由(1)得![]() ,作差得
,作差得![]() ,讨论n可得出
,讨论n可得出![]() 的最大值,再由恒等式思想,建立关于t的不等式,可求得实数
的最大值,再由恒等式思想,建立关于t的不等式,可求得实数![]() 的取值范围.
的取值范围.
(1)设等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,由已知可得
,由已知可得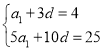 得
得![]() ,
,
所以,![]() ,
,![]() ;
;
(2)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
(3)![]() ,则由
,则由![]() ,
,
①当![]() 时,
时,![]() ,
,
②当![]() 时,
时,![]() .
.
③当![]() 时,
时,![]() ,
,
所以![]() ,所以数列
,所以数列![]() 的最大值为
的最大值为![]() ,
,
又因为![]() 恒成立,所以
恒成立,所以![]() ,所以
,所以![]() 或
或![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某班在一次个人投篮比赛中,记录了在规定时间内投进![]() 个球的人数分布情况:
个球的人数分布情况:
进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
投进 | 1 | 2 | 7 | 2 |
其中![]() 和
和![]() 对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
(1)投进3个球和4个球的分别有多少人?
(2)从进球数为3,4,5的所有人中任取2人,求这2人进球数之和为8的概率.