题目内容
设 ,是否存在
,是否存在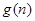 使等式
使等式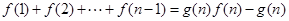 对
对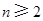 的一切自然数都成立,并证明你的结论.
的一切自然数都成立,并证明你的结论.
【答案】
猜想: .用数学归纳法证明:见解析。
.用数学归纳法证明:见解析。
【解析】
试题分析:解: ,
, ,
, ,
,
由 ,
,
得当 时,
时, ,可得
,可得 .
.
当 时,
时, ,得
,得 .
.
猜想: .
.
用数学归纳法证明:当 时,已验证成立.
时,已验证成立.
假设 (
( ,
, )时成立,即
)时成立,即 ,
,
且有 成立.
成立.
则当 时,
时,


 .
.
即当 时成立.
时成立.
综上可知, 使等式
使等式 对
对 的一切自然数都成立.
的一切自然数都成立.
考点:本题主要考查数学归纳法的概念及方法步骤。
点评:典型题,注意观察式子的结构特点,从K到k+1的变化进行有目的的“配凑”变形。

练习册系列答案
相关题目
 ,是否存在g(n),使等式f(1)+f(2)+…+f(n-1)=g(n)f(n)-1
,是否存在g(n),使等式f(1)+f(2)+…+f(n-1)=g(n)f(n)-1