题目内容
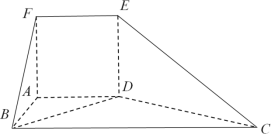
【题目】现拟建一个粮仓,如图1所示,粮仓的轴截而如图2所示,ED=EC,AD![]() BC,BC⊥AB,EF⊥AB,CD交EF于点G,EF=FC=10m.
BC,BC⊥AB,EF⊥AB,CD交EF于点G,EF=FC=10m.
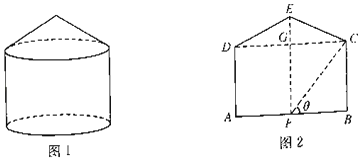
(1)设∠CFB=θ,求粮仓的体积关于θ的函数关系式;
(2)当sinθ为何值时,粮仓的体积最大?
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() 时,粮仓的体积最大.
时,粮仓的体积最大.
【解析】
(1)根据已知条件分别求出![]() ,
,![]() ,再代入体积公式即可.
,再代入体积公式即可.
(2)令![]() ,将(1)问的关系式转化为三次函数,求导即可得到最大值时的正弦值.
,将(1)问的关系式转化为三次函数,求导即可得到最大值时的正弦值.
(1)因为![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 是平行四边形.
是平行四边形.
又因为![]() ,所以四边形
,所以四边形![]() 是矩形,
是矩形,
且![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 是三角形
是三角形![]() 的中线.
的中线.
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
化简得![]() ,
,![]() .
.
(2)令![]() ,
,![]() ,
,
则粮仓的体积![]() ,
,
![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() (舍去),
(舍去),
当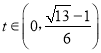 时,
时,![]() 0,y在
0,y在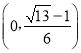 上单调递增;
上单调递增;
当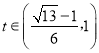 时,
时,![]() ,y在
,y在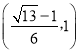 上单调递减,
上单调递减,
所以当![]() 时,即
时,即![]() 时,粮仓的体积最大.
时,粮仓的体积最大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目