题目内容
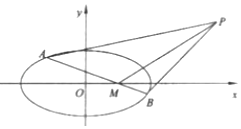
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
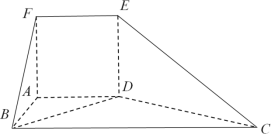
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)线段
;(Ⅲ)线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
【解析】
(I)根据面面垂直的性质定理,证得![]() 平面
平面![]() ,由此证得
,由此证得![]() .(II)以
.(II)以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,通过计算直线
轴建立空间直角坐标系,通过计算直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,由此计算出线面角的正弦值.(III)设
的法向量,由此计算出线面角的正弦值.(III)设![]() ,用
,用![]() 表示出
表示出![]() 点的坐标,利用直线
点的坐标,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量垂直列方程,解方程求得
的法向量垂直列方程,解方程求得![]() 的值,由此判断存在符合题意的点
的值,由此判断存在符合题意的点![]() .
.
解:(Ⅰ)证明:因为![]() 为正方形,
为正方形,
所以![]() .
.
又因为平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)由(Ⅰ)可知,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() 两两垂直.
两两垂直.
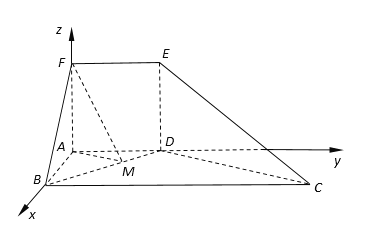
分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 即
即![]()
令![]() ,则
,则![]() ,
,
所以![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() .
.
(Ⅲ)设![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则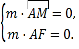
因为![]() ,所以
,所以![]()
令![]() ,则
,则![]() ,所以
,所以![]() .
.
在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() 等价于存在
等价于存在![]() ,使得
,使得![]() .
.
因为![]() ,由
,由![]() ,
,
所以![]() ,
,
解得![]() ,
,
所以线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】近年电子商务蓬勃发展, ![]() 年某网购平台“双
年某网购平台“双![]() ”一天的销售业绩高达
”一天的销售业绩高达![]() 亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出![]() 次成功交易,并对其评价进行统计,网购者对商品的满意率为
次成功交易,并对其评价进行统计,网购者对商品的满意率为![]() ,对快递的满意率为
,对快递的满意率为![]() ,其中对商品和快递都满意的交易为
,其中对商品和快递都满意的交易为![]() 次.
次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对商品满意与对快递满意之间有关系”?
的把握认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取![]() 次交易进行问卷调查,详细了解满意与否的具体原因,并在这
次交易进行问卷调查,详细了解满意与否的具体原因,并在这![]() 次交易中再随机抽取
次交易中再随机抽取![]() 次进行电话回访,听取购物者意见.求电话回访的
次进行电话回访,听取购物者意见.求电话回访的![]() 次交易至少有一次对商品和快递都满意的概率.
次交易至少有一次对商品和快递都满意的概率.
附: 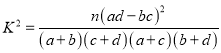 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|