题目内容
设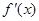 是函数
是函数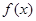 的导函数,将
的导函数,将 和
和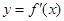 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )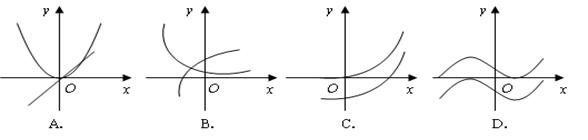
D
解析试题分析:导函数的正负决定函数的增减,所以只有D是不可能正确的.
考点:本小题主要考查导数与函数的单调性的关系,考查学生的读图识图的能力和分析问题、解决问题的能力.
点评:在解决这个题目时,要准确理解导数的正负与函数的单调性之间的关系.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
已知函数 ,正实数
,正实数 满足
满足 ,且
,且 ,若
,若 在区间
在区间 上的最大值为2,则
上的最大值为2,则 的值为( )
的值为( )
A. | B. | C. | D. |
函数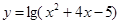 的单调递增区间为( )
的单调递增区间为( )
A.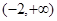 | B.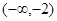 | C.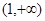 | D.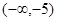 |
已知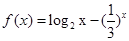 ,若实数
,若实数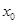 是方程
是方程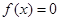 的解,且
的解,且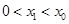 ,则
,则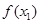 的值是( )
的值是( )
| A.恒为负 | B.等于零 | C.恒为正 | D.不小于零 |
下列各组函数中,f(x)与g(x)表示同一函数的是( )
A.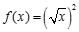 与 与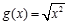 | B.f(x)=x与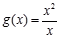 |
C.f(x)=x与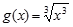 | D.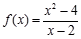 与g(x)=x+2 与g(x)=x+2 |
设函数 上单调递增,则
上单调递增,则 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
设f(x)是R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=
| A.1 | B.3 | C.-1 | D.-3 |
偶函数 在区间
在区间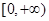 单调增加,则满足
单调增加,则满足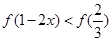 的
的 取值范围是( )
取值范围是( )
A.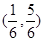 | B.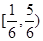 | C.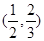 | D. |

 )
)