Question

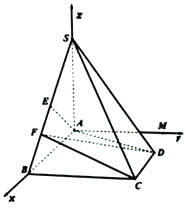
【题目】如图，在四棱锥中， 平面，且， ， 是边的中点．

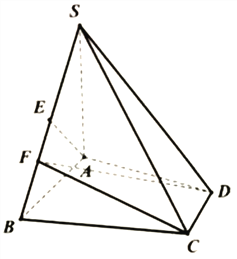
（1）求证： 平面；

（2）若是线段上的动点（不含端点）：问当为何值时，二面角余弦值为．

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）由平面得，再根据，可推出平面，再由及是边的中点，可推出，从而可证平面；（2）在底面内过点作直线， ，以， ， 所在直线分别为， ， 轴，建立空间直角坐标系，由（1） 可得是平面的一个法向量，再求出平面的一个法向量，再根据二面角余弦值为，即可求得.

试题解析：（1）证明：∵平面

∴，

∵， ，

∴平面

∴，

在等腰直角中，∵是边的中点

∴，

∵

∴平面．

（2）解：在底面内过点作直线， ，∵平面，

以， ， 所在直线分别为， ， 轴，建立空间直角坐标系，

∴， ， ， ， ，

∴，

∴，

∵平面

∴是平面的一个法向量，

∵是线段上的动点，设（），

∴，∴，∴，

设是平面的一个法向量，

∴∴

取， ，∴

设二面角大小为，

∴

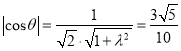
∴，此时二面角是钝二面角，符合题意，此时．