题目内容
如图,已知OPQ是半径为1，圆心角为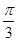
的扇形，C是扇形弧上的动点,ABCD是扇形的内接矩形,记
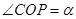,求当角
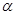取何值时, 矩形ABCD的面积最大?并求出这个最大值.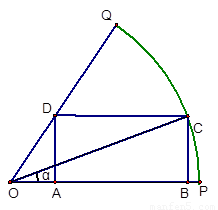
【答案】
= 
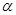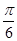矩形ABCD面积的最大值为
。
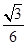【解析】
试题分析：解：由题意可得
在三角形OCB中，OC=1,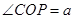
,
所以
BC=sin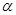 OB=cos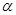
在三角形OAD中，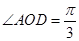
，AD="BC=" sin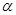
所以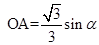 
所以AB="OB-OA="
cos -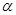 
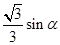5分
则，矩形ABCD的面积为
= 
=
=
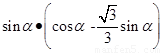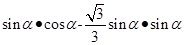
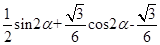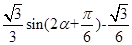
所以矩形ABCD面积的最大值为。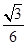
此时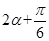
=
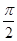
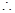
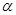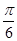= 12分
考点：三角函数的运用
点评：主要是考查了三角函数的实际问题中的运用，属于中档题。
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
如图所示，已知OPQ是半径为1，圆心角为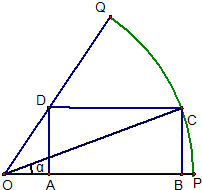
如图，已知OPQ是半径为1，圆心角为
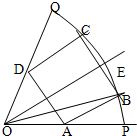如图，已知OPQ是半径为1，圆心角为60°的扇形，∠POQ的平分线交弧PQ于点E，扇形POQ的内接矩形ABCD关于OE对称；设∠POB=α，矩形ABCD的面积为S．
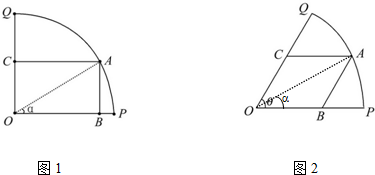如图1所示，已知OPQ是半径为1，圆心角为θ的扇形，A是扇形弧PQ上的动点，AB∥OQ，OP与AB交于点B，AC∥OP，OQ与AC交于点C．记∠AOP=α．