题目内容
如图所示，已知OPQ是半径为1，圆心角为| π | 3 |
分析：先把矩形的各个边长用角α表示出来，进而表示出矩形的面积；再利用角α的范围来求出矩形面积的最大值即可．
解答：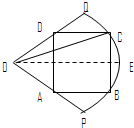
解：设OE交AD于M，交BC于N，显然矩形ABCD关于OE对称，而M，N均为AD，BC的中点，在Rt△ONC中，CN=sinα，ON=cosα．OM=DM/tan
=
DM=
CN=
sinα，∴MN=ON-OM=cosα-
sinα
即AB=cosα-
sinα∴BC=2CN=2sinα
故：S矩=AB•BC=(cosα-
sinα)•2sinα
=2sinαcosα-2
sin2α=sin2α-
(1-cos2α)=sin2α+
cos2α-
=2sin(2α+
)-
∵0＜α＜
，∴0＜2α＜
，
＜2α+
＜
故当2α+
=
，即α=
时，S矩形取得最大，此时S矩形=2-
．
解：设OE交AD于M，交BC于N，显然矩形ABCD关于OE对称，而M，N均为AD，BC的中点，在Rt△ONC中，CN=sinα，ON=cosα．OM=DM/tan| π |
| 6 |
| 3 |
| 3 |
| 3 |
| 3 |
即AB=cosα-
| 3 |
故：S矩=AB•BC=(cosα-
| 3 |
=2sinαcosα-2
| 3 |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
∵0＜α＜
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
故当2α+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 3 |
点评：本题主要考查解三角形的有关知识在实际生活中的应用问题；解决这一类型题目的关键在与把文字语言转化为数学表达式，最终利用数学知识解题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
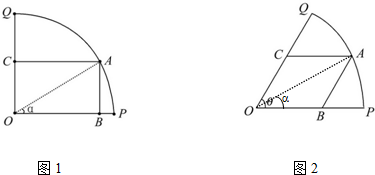如图1所示，已知OPQ是半径为1，圆心角为θ的扇形，A是扇形弧PQ上的动点，AB∥OQ，OP与AB交于点B，AC∥OP，OQ与AC交于点C．记∠AOP=α．
的扇形，C是扇形弧上的动点，ABCD是扇形的内接矩形．记∠COP＝α，求当角α取何值时，矩形ABCD的面积最大？并求出这个最大面积．
如图所示，已知OPQ是半径为1，圆心角为
的扇形，ABCD是扇形的内接矩形，B，C两点在圆弧上，OE是∠POQ的平分线，连接OC，记∠COE=α，问：角α为何值时矩形ABCD面积最大，并求最大面积．
的扇形，ABCD是扇形的内接矩形，B，C两点在圆弧上，OE是∠POQ的平分线，连接OC，记∠COE=α，问：角α为何值时矩形ABCD面积最大，并求最大面积．