题目内容
设函数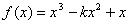
 .
.
(1) 当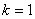 时,求函数
时,求函数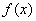 的单调区间;
的单调区间;
(2) 当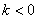 时,求函数
时,求函数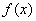 在
在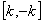 上的最小值
上的最小值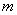 和最大值
和最大值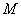 .
.
解:对函数 求导得
求导得 .
.
(1)当 时,
时, ,由
,由 ,
,
可知 ,
,  在
在 上单调递增.
上单调递增.
(2)方法一:当 时,
时, ,
,
其图像开口向上,对称轴 ,且过点
,且过点
(i)当 ,即
,即 时,
时, ,
,
 在
在 上单调递增,从而当
上单调递增,从而当 时,
时, 取得最小值
取得最小值 ,当
,当 时,
时, 取得最大值
取得最大值 .
.
(ii)当 ,即
,即 时,令
时,令 解得
解得 ,
,
注意到 , 所以
, 所以 .
.
因为  ,
,
所以  的最小值
的最小值 ;
;
因为 ,
,
所以  的最大值
的最大值 ;
;
综上所述,当 时,
时, 的最小值
的最小值 ,最大值
,最大值 .
.
方法二:
当 时,对
时,对 ,都有
,都有 ,
,
故  ;
;

 ,
,
故  .
.
又 ,
, ,
,
所以 ,
, 

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 在区间
在区间 上是减函数,那么
上是减函数,那么 的最大值为 .
的最大值为 . 在
在 处取得极值,且在
处取得极值,且在 处的切线平行于
处的切线平行于 ,则
,则 .
. A.8 B. 18 C.26 D.80
A.8 B. 18 C.26 D.80 ,求证:
,求证: .
. 在[a,b]上连续,在(a,b)上可导且
在[a,b]上连续,在(a,b)上可导且 ,则当
,则当 时,有( C )
时,有( C ) B.
B.
 D.
D.
 试求
试求 .
. 围成封闭图形的面积.
围成封闭图形的面积. 在
在 处有极值10,则
处有极值10,则
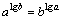 成立;
成立; 的倾斜角等于
的倾斜角等于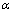
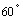 角,则过空间一点P且与a,b均成
角,则过空间一点P且与a,b均成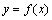 ,若存在常数M>0,使
,若存在常数M>0,使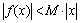 对定义域内的任意x均成立,则称
对定义域内的任意x均成立,则称 为“倍约束函数”。对于函数
为“倍约束函数”。对于函数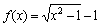 ,该函数是倍约束函数。
,该函数是倍约束函数。