题目内容
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
(1)写出该抛物线的标准方程及其准线方程;
(2)当直线PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
解:(1)由已知条件,可设抛物线的方程为y2=2px.
∵点P(1,2)在抛物线上,∴22=2p1,解得p=2.∴所求抛物线的方程是y2=4x,准线方程是x=-1.
(2)设直线PA的斜率为kPA,直线PB的斜率为kPB.则kPA= (x11),kPB=
(x11),kPB= (x21),
(x21),
∵PA与PB的斜率存在且倾斜角互补,∴kPA=-kPB.由A(x1,y1),B(x2,y2)均在抛物线上,得
y12=4x1,①
y22=4x2,②
∴ =-
=- ,∴y1+2=-(y2+2),∴y1+y2=-4. 由①-②得直线AB的斜率为-1
,∴y1+2=-(y2+2),∴y1+y2=-4. 由①-②得直线AB的斜率为-1

练习册系列答案
相关题目
 的前
的前 项和是
项和是 ,则使
,则使 的最小正整数
的最小正整数 表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大
表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大 B
B  C
C  D
D 
 的子集
的子集 为E的第k个子集,其中k=
为E的第k个子集,其中k= ,则
,则 是E的第 个子集;(2)E的第211个子集是
是E的第 个子集;(2)E的第211个子集是  为奇函数,且当
为奇函数,且当 时,
时, ,则
,则
 B.
B. C.
C. D.
D.
 .
.  满足
满足 ,且
,且 是函数
是函数 的两个零点,则
的两个零点,则 等于
等于 对角线
对角线 ,
, 与
与 交于点
交于点 ,某指数函数
,某指数函数 ,经过点
,经过点 ,则
,则 = ( )
= ( )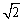
 B.
B. C.
C. D.
D.
