题目内容
【题目】数学家默拉在1765年提出定理，三角形的外心，重心，垂心(外心是三角形三条边的垂直平分线的交点重心是三角形三条中线的交点，垂心是三角形三条高的交点)依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后人称之为三角形的欧拉线，已知△ABC的顶点
，则△ABC的欧拉线方程为____________________
【答案】
【解析】
因为
，所以
外心，重心，垂心都位于线段
的垂直平分线上，由两直线垂直斜率的关系以及两点的斜率公式得出线段的垂直平分线的斜率，由中点坐标公式得出的中点坐标，最后由点斜式写出方程.
因为，所以外心，重心，垂心都位于线段的垂直平分线上
设线段的垂直平分线的斜率为
，则
，
又因为的中点坐标为
所以△ABC的欧拉线方程为
，即
故答案为：
练习册系列答案
春雨教育同步作文系列答案
相关题目
【题目】根据消费者心理学的研究，商品的销售件数与购买人数存在一定的关系，商家可以根据此调整相应的商品小手策略，以谋求商品更多销量，从而获取更多利润.某商场对购买人数和销售件数进行了统计对比，得到如下表格：
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
（参考公式：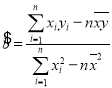
，
）
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图：
（2）根据（1）中所绘制的散点图，可得出购买人数与商品销售件数存在怎样的关系？并求出回归直线方程；（结果保留到小数点后两位）
（3）预测当进店人数为80人时，商品销售的件数.（结果保留整数）
