题目内容
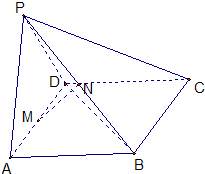 如图,P为菱形ABCD所在平面外一点,M、N 分别为AD、PB 的中点,平面PAD⊥平面ABCD,PA=PD=AD=2,∠DAB=60°求证:
如图,P为菱形ABCD所在平面外一点,M、N 分别为AD、PB 的中点,平面PAD⊥平面ABCD,PA=PD=AD=2,∠DAB=60°求证:(1)MN∥平面PCD
(2)AD⊥PB
(3)求三棱锥D-PBC的体积.
分析:(1)再取PC的中点Q,证明四边形MNQD为平行四边形,可得AM∥DQ,再利用直线和平面平行的判定定理证明 MN∥平面PCD.
(2)由条件可得AN是等腰三角形PAB的底边上的中线,故有AN⊥PB.同理可得,DN⊥PB.利用直线和平面垂直的判定定理可得PB⊥平面AND,从而证得AD⊥PB.
(3)先证得PM⊥平面ABCD,可得PM为三棱锥P-DBC的高线,再根据VD-PBC=VP-BCD=
•S△BCD•PM,运算求得结果.
(2)由条件可得AN是等腰三角形PAB的底边上的中线,故有AN⊥PB.同理可得,DN⊥PB.利用直线和平面垂直的判定定理可得PB⊥平面AND,从而证得AD⊥PB.
(3)先证得PM⊥平面ABCD,可得PM为三棱锥P-DBC的高线,再根据VD-PBC=VP-BCD=
| 1 |
| 3 |
解答:解:(1)再取PC的中点Q,∵四边形ABCD为菱形,M、N 分别为AD、PB 的中点,∴MD平行且等于
BC,NQ平行且等于
BC,
故MD和NQ平行且相等,故四边形MNQD为平行四边形,故 AM∥DQ.
再由 DQ?平面PCD,AM不在平面 PCD内,可得 MN∥平面PCD.
(2)∵四边形ABCD为菱形,PA=PD=AD=2,∠DAB=60°,∴PA=PD=AD=2=AB=BD=CD,
故AN是等腰三角形PAB的底边上的中线,故有AN⊥PB.
同理可得,DN⊥PB.
由于AN和 DN是平面 AND内的两条相交直线,故有PB⊥平面AND.
而AD?平面AND,∴AD⊥PB.
(3)由于平面PAD⊥平面ABCD,△PAD是边长为2的等边三角形,M为AD的中点,故有PM⊥平面ABCD,
故PM为三棱锥P-DBC的高线,且PM=
AD=
,
∴VD-PBC=VP-BCD=
•S△BCD•PM=
•(
•BC•CDsin60°)•PM=
×(
×2×2×
)•
=1.
| 1 |
| 2 |
| 1 |
| 2 |
故MD和NQ平行且相等,故四边形MNQD为平行四边形,故 AM∥DQ.
再由 DQ?平面PCD,AM不在平面 PCD内,可得 MN∥平面PCD.
(2)∵四边形ABCD为菱形,PA=PD=AD=2,∠DAB=60°,∴PA=PD=AD=2=AB=BD=CD,
故AN是等腰三角形PAB的底边上的中线,故有AN⊥PB.
同理可得,DN⊥PB.
由于AN和 DN是平面 AND内的两条相交直线,故有PB⊥平面AND.
而AD?平面AND,∴AD⊥PB.
(3)由于平面PAD⊥平面ABCD,△PAD是边长为2的等边三角形,M为AD的中点,故有PM⊥平面ABCD,
故PM为三棱锥P-DBC的高线,且PM=
| ||
| 2 |
| 3 |
∴VD-PBC=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题主要考查直线和平面平行的判定定理的应用,证明两条直线垂直、以及用等体积法求棱锥的体积,属于中档题.

练习册系列答案
相关题目
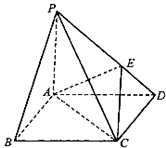 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. (2009•闸北区一模)如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,AB=1,PA•AC=1,∠ABC=θ(0°<θ≤90°).
(2009•闸北区一模)如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,AB=1,PA•AC=1,∠ABC=θ(0°<θ≤90°).
