题目内容
数列 前
前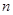 项和为
项和为 ,已知
,已知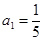 ,且对任意正整数
,且对任意正整数 ,都有
,都有 ,若
,若 恒成立,则实数
恒成立,则实数 的最小值为( )
的最小值为( )
A. | B.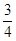 | C.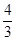 | D.4 |
B
解析试题分析:由am+n=am•an,分别令m和n等于1和1或2和1,由a1求出数列的各项,发现此数列是首项和公比都为 的等比数列,利用等比数列的前n项和的公式表示出Sn,而Sn<a恒成立即n趋于正无穷时,求出Sn的极限小于等于a,求出极限列出关于a的不等式,即可得到a的最小值.解:令m=1,n=1,得到a2=a12=
的等比数列,利用等比数列的前n项和的公式表示出Sn,而Sn<a恒成立即n趋于正无穷时,求出Sn的极限小于等于a,求出极限列出关于a的不等式,即可得到a的最小值.解:令m=1,n=1,得到a2=a12=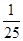 ,同理令m=2,n=1,得到a3=
,同理令m=2,n=1,得到a3=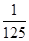 ,所以此数列是首项为
,所以此数列是首项为 ,公比也为
,公比也为 的等比数列…Sn<a恒成立即n→+∞时,Sn的极限≤a,所以
的等比数列…Sn<a恒成立即n→+∞时,Sn的极限≤a,所以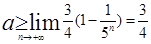 ,故答案为
,故答案为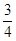
考点:等比数列
点评:此题考查了等比数列关系的确定,掌握不等式恒成立时所满足的条件,灵活运用等比数列的前n项和的公式及会进行极限的运算,是一道综合题.

练习册系列答案
相关题目
已知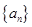 是首项为
是首项为 的等比数列,
的等比数列, 是
是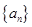 的前
的前 项和,且
项和,且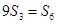 .则
.则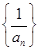 的前
的前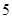 项和为.
项和为.
A. 或 或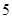 | B.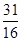 或 或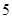 | C.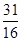 | D. |
在等比数列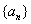 中,若
中,若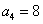 ,
,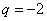 ,则
,则 的值为( )
的值为( )
A.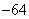 | B.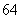 | C. | D.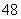 |
若等比数列{a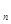 }的前三项和为13,首项为1,则其公比为
}的前三项和为13,首项为1,则其公比为
| A.2或-1 | B.3或-4 | C.4或-3 | D.3 |
已知正项等比数列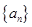 满足:
满足: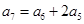 ,若存在两项
,若存在两项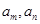 使得
使得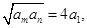 则
则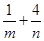 的最小值为( ).
的最小值为( ).
A.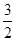 | B.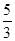 | C.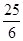 | D.不存在 |
在数列 中,
中,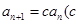 为非零常数),且前
为非零常数),且前 项和为
项和为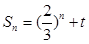 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C.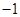 | D.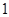 |
若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,则a3+a5的值为
| A.5 | B.10 | C.15 | D.20 |
若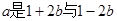 的等比中项,则
的等比中项,则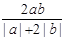 的最大值为( )
的最大值为( )
A.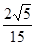 | B.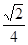 | C.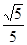 | D.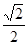 |
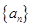 中,
中, ,
, ,
, ,则
,则 ( )
( )