题目内容
已知向量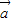 =(1,1),向量
=(1,1),向量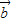 与
与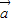 的夹角为
的夹角为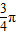 ,且
,且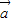 •
•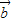 =-1.
=-1.(1)求:向量
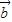 ;
;(2)若
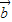 与
与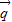 =(1,0)的夹角为
=(1,0)的夹角为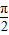 ,而向量
,而向量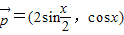 ,试求f(x)=
,试求f(x)=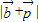 ;
;(3)已知△ABC的三边长a、b、c满足b2=ac且b所对的角为x,求此时(2)中的f(x)的取值范围.
【答案】分析:(1)设出向量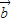 =(x,y),利用向量
=(x,y),利用向量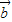 与
与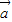 的夹角为
的夹角为 ,且
,且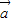 •
•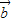 =-1.得到 x+y=-1与 x2+y2=1,解方程求出x,y即可.
=-1.得到 x+y=-1与 x2+y2=1,解方程求出x,y即可.
(2)利用(1)以及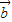 与
与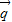 =(1,0)的夹角为
=(1,0)的夹角为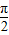 ,判断
,判断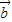 =(0,-1),表示
=(0,-1),表示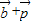 ,然后利用向量的模的求法求出
,然后利用向量的模的求法求出
f(x)=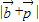 .
.
(3)通过余弦定理以及b2=ac,求出1≥cosx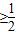 ,通过函数的单调性求出f(x)的值域即可.
,通过函数的单调性求出f(x)的值域即可.
解答:解:(1)设向量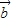 =(x,y)
=(x,y)
∵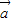 •
•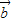 =-1,
=-1,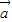 •
•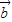 =|a||
=|a||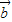 |cosΘ=1×x+1×y=x+y
|cosΘ=1×x+1×y=x+y
∴x+y=-1…①
∵|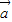 ||
||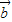 |cos
|cos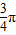 =-
=-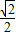 |
|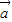 ||
||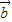 |=-
|=-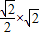 |
|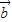 |=-|
|=-|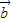 |
|
∴|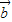 |=1
|=1
∴x2+y2=1…②
①代入②得:
x2+(-x-1)2=1
可得 2x2+2x=0
x(x+1)=0,
∴x₁=0,x2=-1
y₁=-1,y2=0
∴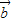 =(0,-1),或
=(0,-1),或 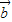 =(-1,0)
=(-1,0)
(2)因为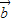 与
与 =(1,0)的夹角为
=(1,0)的夹角为 ,所以
,所以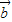 =(0,-1),
=(0,-1),
因为向量 ,
,
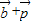 =
= ,
,
所以f(x)=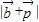 =
=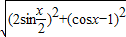 =
=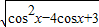
(3)因为△ABC的三边长a、b、c满足b2=ac且b所对的角为x,
所以b2=a2+c2-2accosx,
∴ac=a2+c2-2accosx,ac+2accosx≥2ac,解得1≥cosx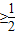 ,
,
f(x)=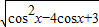 ,1≥cosx
,1≥cosx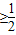 ,
,
因为f(x)=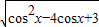 =
=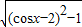 在1≥cosx
在1≥cosx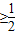 上是减函数,
上是减函数,
所以f(x)∈[0,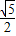 ]
]
点评:本题是中档题,考查向量的数量积的两种计算方法的应用,向量的模的求法,余弦定理以及二次函数的最值的求法,难度比较大的综合题.
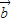 =(x,y),利用向量
=(x,y),利用向量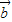 与
与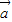 的夹角为
的夹角为 ,且
,且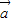 •
•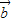 =-1.得到 x+y=-1与 x2+y2=1,解方程求出x,y即可.
=-1.得到 x+y=-1与 x2+y2=1,解方程求出x,y即可.(2)利用(1)以及
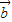 与
与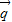 =(1,0)的夹角为
=(1,0)的夹角为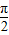 ,判断
,判断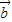 =(0,-1),表示
=(0,-1),表示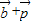 ,然后利用向量的模的求法求出
,然后利用向量的模的求法求出f(x)=
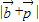 .
.(3)通过余弦定理以及b2=ac,求出1≥cosx
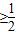 ,通过函数的单调性求出f(x)的值域即可.
,通过函数的单调性求出f(x)的值域即可.解答:解:(1)设向量
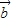 =(x,y)
=(x,y)∵
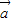 •
•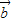 =-1,
=-1,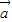 •
•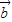 =|a||
=|a||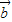 |cosΘ=1×x+1×y=x+y
|cosΘ=1×x+1×y=x+y∴x+y=-1…①
∵|
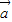 ||
||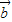 |cos
|cos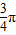 =-
=-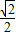 |
|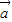 ||
||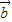 |=-
|=-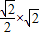 |
|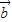 |=-|
|=-|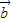 |
|∴|
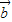 |=1
|=1∴x2+y2=1…②
①代入②得:
x2+(-x-1)2=1
可得 2x2+2x=0
x(x+1)=0,
∴x₁=0,x2=-1
y₁=-1,y2=0
∴
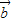 =(0,-1),或
=(0,-1),或 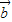 =(-1,0)
=(-1,0)(2)因为
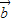 与
与 =(1,0)的夹角为
=(1,0)的夹角为 ,所以
,所以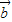 =(0,-1),
=(0,-1),因为向量
 ,
,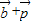 =
= ,
,所以f(x)=
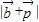 =
=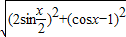 =
=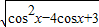
(3)因为△ABC的三边长a、b、c满足b2=ac且b所对的角为x,
所以b2=a2+c2-2accosx,
∴ac=a2+c2-2accosx,ac+2accosx≥2ac,解得1≥cosx
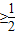 ,
,f(x)=
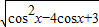 ,1≥cosx
,1≥cosx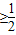 ,
,因为f(x)=
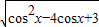 =
=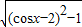 在1≥cosx
在1≥cosx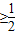 上是减函数,
上是减函数,所以f(x)∈[0,
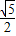 ]
]点评:本题是中档题,考查向量的数量积的两种计算方法的应用,向量的模的求法,余弦定理以及二次函数的最值的求法,难度比较大的综合题.

练习册系列答案
相关题目