题目内容
已知向量 =(sinθ,cosθ-2sinθ),
=(sinθ,cosθ-2sinθ), =(1,2)
=(1,2)
(1)若 ⊥
⊥ ,求tanθ的值;
,求tanθ的值;
(2)若 ∥
∥ ,且θ为第Ⅲ象限角,求sinθ和cosθ的值.
,且θ为第Ⅲ象限角,求sinθ和cosθ的值.
解:(1)∵向量 =(sinθ,cosθ-2sinθ),
=(sinθ,cosθ-2sinθ), =(1,2),
=(1,2), ⊥
⊥ ,
,
∴ =sinθ+2cosθ-4sinθ=0,解得tanθ=
=sinθ+2cosθ-4sinθ=0,解得tanθ= .…(6分)
.…(6分)
(2)∵ ∥
∥ ,向量
,向量 =(sinθ,cosθ-2sinθ),
=(sinθ,cosθ-2sinθ), =(1,2),
=(1,2),
∴2sinθ-(cosθ-2sinθ)=0,化简可得tanθ= .
.
再由θ为第Ⅲ象限角以及sin2θ+cos2θ=1,
解得sinθ=-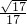 ,cosθ=-
,cosθ=-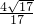 . …(6分)
. …(6分)
分析:(1)根据两个向量垂直的性质可得 =sinθ+2cosθ-4sinθ=0,由此解得tanθ的值.
=sinθ+2cosθ-4sinθ=0,由此解得tanθ的值.
(2)根据两个向量共线的性质可得2sinθ-(cosθ-2sinθ)=0,由此求得tanθ的值,再由sin2θ+cos2θ=1,
以及θ为第Ⅲ象限角求得sinθ和cosθ的值.
点评:本题主要考查两个向量共线、垂直的性质,同角三角函数的基本关系,属于基础题.
 =(sinθ,cosθ-2sinθ),
=(sinθ,cosθ-2sinθ), =(1,2),
=(1,2), ⊥
⊥ ,
,∴
 =sinθ+2cosθ-4sinθ=0,解得tanθ=
=sinθ+2cosθ-4sinθ=0,解得tanθ= .…(6分)
.…(6分)(2)∵
 ∥
∥ ,向量
,向量 =(sinθ,cosθ-2sinθ),
=(sinθ,cosθ-2sinθ), =(1,2),
=(1,2),∴2sinθ-(cosθ-2sinθ)=0,化简可得tanθ=
 .
.再由θ为第Ⅲ象限角以及sin2θ+cos2θ=1,
解得sinθ=-
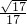 ,cosθ=-
,cosθ=-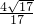 . …(6分)
. …(6分)分析:(1)根据两个向量垂直的性质可得
 =sinθ+2cosθ-4sinθ=0,由此解得tanθ的值.
=sinθ+2cosθ-4sinθ=0,由此解得tanθ的值.(2)根据两个向量共线的性质可得2sinθ-(cosθ-2sinθ)=0,由此求得tanθ的值,再由sin2θ+cos2θ=1,
以及θ为第Ⅲ象限角求得sinθ和cosθ的值.
点评:本题主要考查两个向量共线、垂直的性质,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目