题目内容
【题目】已知△ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:
(1)2sinBcosC﹣sin(B﹣C)的值;
(2)若a=2,求△ABC周长的最大值.
【答案】
(1)解:∵b2+c2=a2+bc,∴a2=b2+c2﹣bc,
结合余弦定理知cosA= ![]() =
= ![]() =
= ![]() ,
,
又A∈(0,π),∴A= ![]() ,
,
∴2sinBcosC﹣sin(B﹣C)=sinBcosC+cosBsinC
=sin(B+C)=sin[π﹣A]=sinA= ![]()
(2)解:由a=2,结合正弦定理得:
![]() =
= ![]() =
= ![]() ,
,
∴b= ![]() sinB,c=
sinB,c= ![]() sinC,
sinC,
则a+b+c=2+ ![]() sinB+
sinB+ ![]() sinC
sinC
=2+ ![]() sinB+
sinB+ ![]() sin(
sin( ![]() ﹣B)
﹣B)
=2+2 ![]() sinB+2cosB=2+4sin(B+
sinB+2cosB=2+4sin(B+ ![]() ),
),
可知周长的最大值为6
【解析】(1)根据余弦定理表示出cosA,把已知得等式变形后代入即可求出cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,然后把所求的式子利用两角和与差的正弦函数公式及诱导公式化简,将sinA的值代入即可求出值;(2)由a=2和sinA的值,根据正弦定理表示出b和c,代入三角形的周长a+b+c中,利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域即可得到周长的最大值.

【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中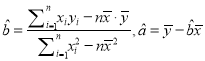 )
)
