题目内容
甲、乙两个人独立地破译密码的概率分别为![]() 和
和![]() ,求:
,求:
(1)两个人都译出密码的概率;
(2)两个人都译不出密码的概率;
(3)恰有一人译出密码的概率.
答案:
解析:
解析:
|
解:A=“甲独立地译出密码”,B=“乙独立地译出密码”,且P(A)= (1)两个人都译出密码的概率为 P(AB)=P(A)P(B)= (2)两个人都译不出密码的概率为 P( = (3)恰有1人译出密码可分为两类: 甲译出密码而乙未译出密码,其概率为 P(A· = 乙译出密码而甲未译出密码,其概率为 P( 综上,知恰有一人译出密码的概率为P(A· 思路分析:我们把“甲独立地译出密码”记为事件A,把“乙独立地译出密码”记为事件B,显然A与B相互独立,同时 |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
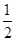 和
和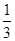 , 求:
, 求: