题目内容
甲、乙两个人独立地破译密码的概率分别为(1)两个人都译出密码的概率;
(2)两个人都译不出密码的概率;
(3)恰有一人译出密码的概率.
思路分析:我们把“甲独立地译出密码”记为事件A,把“乙独立地译出密码”记为事件B,显然A与B相互独立,同时![]() 与B,A与
与B,A与![]() ,
,![]() 与
与![]() 亦相互独立.
亦相互独立.
解:A=“甲独立地译出密码”,B=“乙独立地译出密码”,且P(A)=![]() ,P(B)=
,P(B)=![]() .
.
(1)两个人都译出密码的概率为P(AB)=P(A)P(B)=![]() ×
×![]() =
=![]() .
.
(2)两个人都译不出密码的概率为P(![]() )=P(
)=P(![]() )P(
)P(![]() )=[1-P(A)][1-P(B)]=(1-
)=[1-P(A)][1-P(B)]=(1-![]() )(1-
)(1-![]() )=
)=![]() .
.
(3)恰好1个译出密码可分为两类,即A![]() 与
与![]() B且两类事件为互斥事件:
B且两类事件为互斥事件:
P(A![]() +
+![]() B)=P(
B)=P(![]() B)+P(A
B)+P(A![]() )=P(
)=P(![]() )P(B)+P(A)P(
)P(B)+P(A)P(![]() )=(1-
)=(1-![]() )×
)×![]() +
+![]() (1-
(1-![]() )=
)=![]() .
.

练习册系列答案
相关题目
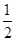 和
和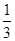 , 求:
, 求: