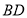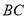题目内容
已知关于 的方程
的方程 :
: ,
, R.
R.
(Ⅰ)若方程 表示圆,求
表示圆,求 的取值范围;
的取值范围;
(Ⅱ)若圆 与直线
与直线 :
: 相交于
相交于 两点,且
两点,且 =
= ,求
,求 的值.
的值.
(Ⅰ)  ;(Ⅱ) 1
;(Ⅱ) 1
【解析】
试题分析:(Ⅰ) 法一:方程 表示圆时,则
表示圆时,则 ,解不等式即可求
,解不等式即可求 的取值范围;法二:可将方程转化为圆的标准方程形式,根据半径的平方大于0求
的取值范围;法二:可将方程转化为圆的标准方程形式,根据半径的平方大于0求 的取值范围。(Ⅱ)用点到线的距离公式求圆心到直线
的取值范围。(Ⅱ)用点到线的距离公式求圆心到直线 的距离,再根据数形结合用勾股定理求
的距离,再根据数形结合用勾股定理求 的值。
的值。
试题解析:【解析】
(1)方程 可化为
可化为  ,2分
,2分
显然  时方程
时方程 表示圆.4分
表示圆.4分
(2)圆的方程化为 ,
,
圆心 (1,2),半径
(1,2),半径  ,6分
,6分
则圆心 (1,2)到直线l:
(1,2)到直线l:  的距离为
的距离为
 .8分
.8分
 ,有
,有  ,
,
 10分
10分
得  .12分
.12分
考点:圆的方程及其弦长问题。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目