题目内容
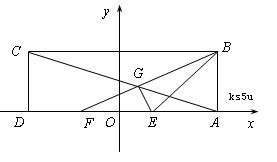
在矩形![]() 中,已知
中,已知![]() ,
,![]() ,E、F为
,E、F为![]() 的两个三等分点,
的两个三等分点,![]() 和
和![]() 交于点
交于点![]() ,
,![]() 的外接圆为⊙
的外接圆为⊙![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 中点
中点![]() 为坐标原点,建立如图所示的平面直角坐标系.
为坐标原点,建立如图所示的平面直角坐标系.
(1)求以F、E为焦点,![]() 和
和![]() 所在直线为准线的椭圆的方程;
所在直线为准线的椭圆的方程;
(2)求⊙![]() 的方程;
的方程;
(3)设点![]() ,过点P作直线与⊙
,过点P作直线与⊙![]() 交于M,N两点,若点M恰好是线段PN的中点,求实数
交于M,N两点,若点M恰好是线段PN的中点,求实数![]() 的取值范围.
的取值范围.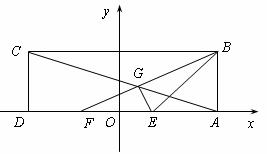
⑴当![]() 时,由已知得
时,由已知得
![]() ,
,![]() ,
,![]() ,
,
因为![]() 是等差数列,所以
是等差数列,所以![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,
,
即![]() ,所以
,所以![]() ,解得
,解得![]() ,或
,或![]() .…………………2分
.…………………2分
当![]() 时,
时,![]() ,对
,对![]() ,
,![]() 成立,所以数列
成立,所以数列![]() 是等差数列;
是等差数列;
当![]() 时,
时,![]() ,对
,对![]() ,
,![]() 成立,所以数列
成立,所以数列![]() 是等差数列;
是等差数列;
所以数列![]() 的通项公式分别为
的通项公式分别为![]() 或
或![]() .…………………………………4分
.…………………………………4分
⑵因为![]() 是等比数列,所以
是等比数列,所以![]() ,
,![]() ,
,![]() 成等比数列,所以
成等比数列,所以![]() ,
,
即![]() ,化简得
,化简得![]() ,所以
,所以![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,不满足
,不满足![]() .
.
当![]() 时,若
时,若![]() ,则与
,则与![]() 矛盾,所以
矛盾,所以![]() ,因此
,因此![]() .……………8分
.……………8分
则![]() ,因为
,因为![]() 按某种顺序排列成等差数列,
按某种顺序排列成等差数列,
所以有![]() ,或
,或![]() ,或
,或![]() ,
,
解之得![]() 或
或![]() 或
或![]() .………………………………………………………12分
.………………………………………………………12分
又因为![]() ,所以
,所以![]() ,所以
,所以 ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
因为![]() 是正整数,所以
是正整数,所以![]() 的取值集合为
的取值集合为![]() .……………………………………16分
.……………………………………16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
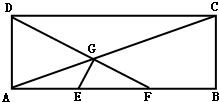 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系,
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系, 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: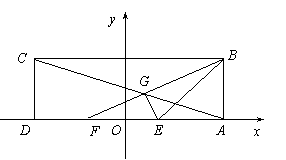 (3)设点
(3)设点