Question

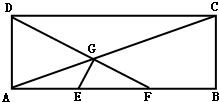如图，在矩形ABCD中，已知AB=3，AD=1，E、F分别是AB的两个三等分点，AC，DF相交于点G，建立适当的平面直角坐标系，
证明：E G⊥D F．

Answer 1

分析：首先根据已知图形建立适当的坐标系如图，然后把需要用到的点的坐标分别表示出来，最后根据向量垂直的定义进行证明．

解答：解：以A为原点，AB所在直线为x轴，建立平面直角坐标系．
则A（0，0）．B（3，0）．C（3，1）．
D（0，1）．E（1，0）．F（2，0）．
由A（0，0）．C（3，1）
知直线AC的方程为：x-3y=0，
由D（0，1）．F（2，0）
知直线DF的方程为：x+2y-2=0，
由

x-3y=0 x+2y-2=0.

得

x= 6 5 y= 2 5 .

故点G点的坐标为(

6

5

，

2

5

)．
又点E的坐标为（1，0），故k_EG=2，
所以k_DF•k_EG=-1．即证得：EG⊥DF

点评：本题考查直线的一般方程与直线的垂直关系，涉及平面向量的计算，通过设置坐标系进行计算，属于基础题．