题目内容
13.已知偶函数f(x)的定义域为{x|x∈R且x≠0},f(x)=$\left\{\begin{array}{l}{2^{|x-1|}}-1,0<x≤2\\ \frac{1}{2}f(x-2),x>2\end{array}\right.$,则函数g(x)=4f(x)-log7(|x|+1)的零点个数为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 令g(x)=0得f(x)=$\frac{1}{4}$log7(|x|+1),分别作出f(x)和y=$\frac{1}{4}$log7(|x|+1)在(0,+∞)上的函数图象,根据函数的图象和奇偶性得出零点个数.
解答 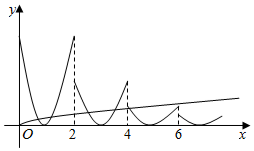 解令g(x)=0得f(x)=$\frac{1}{4}$log7(|x|+1),
解令g(x)=0得f(x)=$\frac{1}{4}$log7(|x|+1),
作出y=f(x)和y=$\frac{1}{4}$log7(|x|+1)在(0,8)上的函数图象如图所示,
由图象可知y=f(x)和y=$\frac{1}{4}$log7(|x|+1)在(0,+∞)上有6个交点,
∴g(x)在(0,+∞)上有6个零点,
∵f(x),g(x)均是偶函数,
∴g(x)在定义域上共有12个零点,
故选:D
点评 本题考查了函数的零点个数判断,正确作出f(x)的图象是解题关键.考查函数思想;数形结合;函数的性质及应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
8.已知(a+x)11=a0+a1(1-x)+a2(1-x)2+…+a11(1-x)11(m>0),|a0|+|a1|+|a2|+…+|a11|=311,则a9=( )
| A. | -220 | B. | 220 | C. | -440 | D. | 440 |
1.函数f(x)=($\frac{1}{2}$)x-x+2的零点所在的一个区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
18.某企业A向杜会迸行融资,先让个人B借给企业a万元(a>0),再从出借日的下个月开始,分成12个月,按月复利1%计算,每月企业等额返还给个人B,现企业A前6个月已按约定返还给个人B,由于某种特殊原因该融资必须停止,企业退还给B $\frac{a}{2}$万元,则该退还方式( )
| A. | 公平 | B. | 企业A吃亏 | C. | 个人B吃亏 | D. | 谁吃亏与a有关 |
2.某学校为了了解高一、高二、高三三个年级的学生的课外阅读时间是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |