题目内容
已知点A(-3,4),B(3,2),过点P(2,-1)的直线L与线段AB有公共点,则直线L的斜率k的取值范围是 .
分析:根据两点间的斜率公式,利用数形结合即可求出直线斜率的取值范围.
解答:解:∵ 点A(-3,4),B(3,2),过点P(2,-1)的直线L与线段AB有公共点,
点A(-3,4),B(3,2),过点P(2,-1)的直线L与线段AB有公共点,
∴直线l的斜率k≥kPB或k≤kPA,
∵PA的斜率为
=
=-1,PB的斜率为
=
=3,
∴直线l的斜率k≥3或k≤-1,
故答案为:k≥3或k≤-1.
 点A(-3,4),B(3,2),过点P(2,-1)的直线L与线段AB有公共点,
点A(-3,4),B(3,2),过点P(2,-1)的直线L与线段AB有公共点,∴直线l的斜率k≥kPB或k≤kPA,
∵PA的斜率为
| -1-4 |
| 2-(-3) |
| -5 |
| 5 |
| -1-2 |
| 2-3 |
| -3 |
| -1 |
∴直线l的斜率k≥3或k≤-1,
故答案为:k≥3或k≤-1.
点评:本题主要考查直线的斜率的求法,利用数形结合是解决本题的关键,比较基础.

练习册系列答案
相关题目
已知点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值等于( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知点A(3,4),B(6,m)到直线3x+4y-7=0的距离相等,则实数m等于( )
A、
| ||||
B、-
| ||||
| C、1 | ||||
D、
|
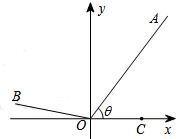 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.