题目内容
【题目】已知圆
经过
，
两点，且圆心在直线
上.
(1)求圆的方程
(2)从原点向圆作切线，求切线方程及切线长.
【答案】(1) 
(或写成:
)；(2)
，
.
【解析】
(1) 解法一: 设圆的方程为
,将
，
两点代入得:
,根据圆的一般方程的圆心为: 
,代入
,
联立方程即可求出答案.
解法二:设根据题意,分析可得圆
的圆心是线段
的垂直平分线与直线的交点,先求出线段的垂直平分线的方程,与直线联立可得圆的圆心的坐标,在由两点间距离公式: 
,代入圆的标准方程:
即可得出答案.
(2) 解法一:过原点的直线中，当斜率不存在时，不与圆相切，当斜率存在时，可设直线方程为
:
,直线圆线切,联立方程:
将其化为关于
的一元二次方程,由题意可知此方程的
,解得
,即可求出切线方程及切线长.
解法二: 过原点的直线中，当斜率不存在时，不与圆相切，当斜率存在时，可设直线方程为:.因为直线与圆相切，故圆心到直线的距离等于半径,根据点到直线的距离公式: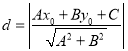
可求得圆的圆心到:的距离为1,可解得 ,即可求出切线方程及切线长.
(1)解法一:设圆的方程为
由题意:
①
②
又圆心在直线
上
故
， ③
由①②③解得:
，
，
，
圆的方程为:(或写成:)，
解法二:由题意，圆心在的中垂线
上，
又在已知直线上，
解得圆心坐标为
，
于是半径
所求圆的方程为:;
(2)解法一:过原点的直线中，当斜率不存在时，不与圆相切
当斜率存在时，设直线方程为
代入
得
即
令
，
解得
，
即切线方程为.
对应切线长为
.
解法二:过原点的直线中，当斜率不存在时，不与圆相切；
当斜率存在时，设直线方程为，
因为直线与圆相切，故圆心到直线的距离等于半径，
根据点到直线的距离公式: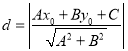可得
解得.即切线方程为.
对应切线长为.
综上所述: 切线方程为,切线长为.
练习册系列答案
阅读快车系列答案
相关题目
