题目内容
一个正方体和一个圆柱等高,并且侧面积相等,则正方体与圆柱的体积比是( )A.π:4
B.4:π
C.1:1
D.π2:4
【答案】分析:先设下正方体的棱长为a,圆柱的底面半径为r,利用圆柱和正方体的侧面积公式可得2πra=4a2,从而得出r与a的关系式,最后利用体积公式即可得出正方体与圆柱的体积比.
解答:解:设下正方体的棱长为a,圆柱的底面半径为r,
由圆柱和正方体的侧面积公式可知,
圆柱侧面积=2πra,正方体的侧面积=4a2,
∵它们的侧面积相等,∴2πra=4a2,∴r=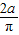 ;
;
∴正方体与圆柱的体积比是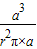 =
=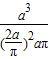 =π:4.
=π:4.
故选A.
点评:此题主要考查圆柱和正方体的表面积及体积公式,属于基础题.
解答:解:设下正方体的棱长为a,圆柱的底面半径为r,
由圆柱和正方体的侧面积公式可知,
圆柱侧面积=2πra,正方体的侧面积=4a2,
∵它们的侧面积相等,∴2πra=4a2,∴r=
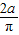 ;
;∴正方体与圆柱的体积比是
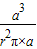 =
=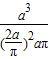 =π:4.
=π:4.故选A.
点评:此题主要考查圆柱和正方体的表面积及体积公式,属于基础题.

练习册系列答案
相关题目