题目内容
已知集![]() 合
合![]() ,
,![]() .
.
(1) 若![]() ,求实数a的取值范围;
,求实数a的取值范围;
(2) 集合![]() ,
,![]() 能否相等?若能,求出a的值;若不能,请说明理由.
能否相等?若能,求出a的值;若不能,请说明理由.
解:![]()
![]()
![]() ,
,![]()
![]() .
.
①当![]() 时,
时,![]() ,所以
,所以![]() 不可能;
不可能;
②当![]() 时,
时,![]() ,若
,若![]() ,则
,则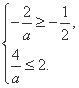 解得
解得![]() .
.
③当![]() 时,
时,![]() ,若
,若![]() ,则
,则 解得
解得![]() .
.
综上所得,a的取值范围为![]() .
.
(2)![]() 分析一:求出满足
分析一:求出满足![]() 时a的取值范围,再与(1)取交集.
时a的取值范围,再与(1)取交集.
解法一:①当![]() 时,
时,![]() ,所以
,所以![]() 成立;
成立;
②当![]() 时,
时,![]() ,若
,若![]() ,则
,则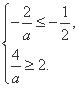 解得
解得![]() .
.
③当![]() 时,
时,![]() ,若
,若![]() ,则
,则 解得
解得![]()
![]() .
.
综上,![]() 时,
时,![]() .
.
![]() 且
且![]() ,
,![]() 若
若![]() ,则
,则![]() 且
且![]() ,矛盾.
,矛盾.
所以,集合![]() 与
与![]()
![]() 不可能相等.
不可能相等.
分析二:利用两个相等集合中元素的对应关系,建立等量关系.
解法二:①当![]() 时,
时,![]() ,所以
,所以![]() ;
;
②当![]() 时,
时,![]() ,若
,若![]() ,则
,则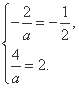 无解.
无解.
③当![]() 时,
时,![]() ,若
,若![]() ,显然不成立.
,显然不成立.
综上,集合![]() 与
与![]() 不可能相等.
不可能相等.

练习册系列答案
相关题目