题目内容
过点P(1，0)的直线l与曲线C：
+y2=1交于A、B两点,试求||PA|-|PB||的最大值.
解析：由题设可知：l：
(t为参数)(α∈［0,π)),
则(1+t cosα)2+2t2 sin2α-2=0,
即(1+sin2α)t2+2t cosα-1=0,
由t的几何意义可得
||PA|-|PB||=|t1+t2|
=|
|=|
|=|
|,
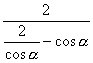令t=cos α∈(-1,1］,
∴f(t)=
-t,f′(t)=-
-1＜0.
∴f(t)是减函数.
∴f(t)min=f(1)=1.故所求最大值为2.
练习册系列答案
相关题目
过点A（a,0）,B(0,b)的直
，原点到该直线的距离为
.
求直线MN的方程；
交椭圆于P、Q两点，以PQ为直径的圆过点D（1，0）？若存在，求出k的值；若不存在，请说明理由。
已知抛物线C的顶点在原点, 焦点为F(0, 1).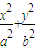
=1（a＞b＞0）离心率为
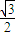，且过P（
，
）．
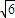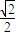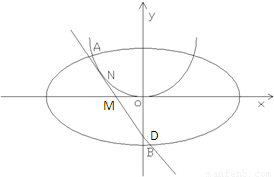
，0），且与开口朝上，顶点在原点的抛物线C切于第二象限的一点N，直 线l与椭圆E交于A，B两点，与y轴交与D点，若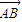
=
，
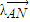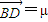
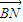，且λ+μ=
，求抛物线C的标准方程．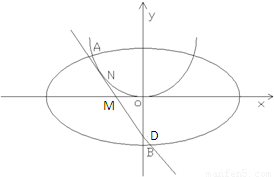
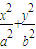=1（a＞b＞0）离心率为
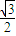，且过P（
，
）．
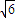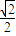，0），且与开口朝上，顶点在原点的抛物线C切于第二象限的一点N，直 线l与椭圆E交于A，B两点，与y轴交与D点，若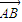
=
，
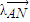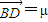
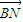，且λ+μ=
，求抛物线C的标准方程．