题目内容
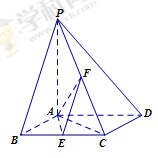
如图,已知四棱锥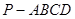 中,底面
中,底面 为菱形,
为菱形,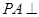 平面
平面 ,
,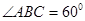 ,
,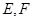 分别是
分别是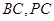 的中点.
的中点.
(1)证明: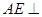 平面
平面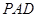 ;
;
(2)取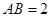 ,若
,若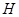 为
为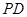 上的动点,
上的动点,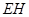 与平面
与平面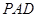 所成最大角的正切值为
所成最大角的正切值为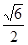 ,求二面角
,求二面角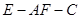 的余弦值。
的余弦值。
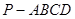 中,底面
中,底面 为菱形,
为菱形,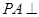 平面
平面 ,
,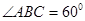 ,
,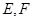 分别是
分别是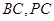 的中点.
的中点.
(1)证明:
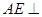 平面
平面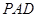 ;
;(2)取
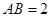 ,若
,若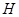 为
为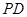 上的动点,
上的动点,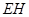 与平面
与平面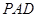 所成最大角的正切值为
所成最大角的正切值为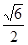 ,求二面角
,求二面角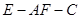 的余弦值。
的余弦值。(1)详见解析;(2)

试题分析:(1)用线面垂直证
 ,用等腰三角形中线即为高线证
,用等腰三角形中线即为高线证 即
即 ,根据线面垂直得判定定理即可得证。(2)由(1)知
,根据线面垂直得判定定理即可得证。(2)由(1)知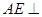 平面
平面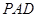 ,则
,则 为
为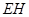 与平面
与平面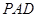 所成的角。因为
所成的角。因为 为定值,所以
为定值,所以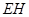 最短即
最短即 最短时角的正弦值最大。故此时
最短时角的正弦值最大。故此时 。故此可推导出
。故此可推导出 的值,过
的值,过 作
作 于
于 ,则
,则 平面
平面 ,过
,过 作
作 于
于 ,连接
,连接 ,则
,则 为二面角
为二面角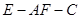 的平面角。也可采用空间向量法。
的平面角。也可采用空间向量法。试题解析:解:方法一:(1)证明:由四边形
 为菱形,
为菱形,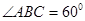 ,可得
,可得 为正三角形,因为
为正三角形,因为 为
为 的中点,
的中点,所以
 1分
1分又
 ,因此
,因此 2分
2分因为
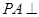 平面
平面 ,
,
 平面
平面 ,
,所以
 3分
3分而

 平面
平面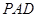 ,
,
 平面
平面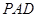
 ,
,所以
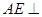 平面
平面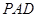 . 5分
. 5分(2)
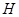 为
为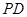 上任意一点,连接
上任意一点,连接 由(1)知
由(1)知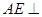 平面
平面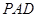 ,则
,则 为
为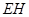 与平面
与平面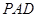 所成的角 6分
所成的角 6分在
 中,
中, ,
,所以当
 最短时,即当
最短时,即当 时,
时, 最大 . 7分
最大 . 7分此时
 , 因此
, 因此
又
 ,所以
,所以 ,
,所以
 8分
8分因为
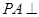 平面
平面 ,
,
 平面
平面 ,
,所以平面
 平面
平面
过
 作
作 于
于 ,则
,则 平面
平面 ,
,过
 作
作 于
于 ,连接
,连接 ,则
,则 为二面角
为二面角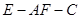 的平面角, 10分
的平面角, 10分在
 中,
中,
又
 是
是 的中点,在
的中点,在 中,
中, 
又
 11分
11分在
 中,
中,
即所求二面角的余弦值为
 。 13分
。 13分第二问:方法二
(2)由(1)可知
 两两垂直,
两两垂直,以
 为坐标原点,建立如图所示的空间直角坐标系。
为坐标原点,建立如图所示的空间直角坐标系。 设
 ,则
,则
 (其中
(其中 ) 6分
) 6分
面
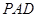 的法向量为
的法向量为


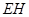 与平面
与平面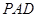 所成最大角的正切值为
所成最大角的正切值为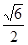 7分
7分
 的最大值为
的最大值为 ,
,即
 在
在 的最小值为
的最小值为 ,
, 函数
函数 对称轴
对称轴 ,
,所以

 ,计算可得
,计算可得 9分
9分所以

设平面
 的一个法向量为
的一个法向量为 ,则
,则
因此
 ,取
,取 ,则
,则 11分
11分 为平面
为平面 的一个法向量. 12分
的一个法向量. 12分所以

所以,所求二面角的余弦值为
 13分
13分
练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 为矩形,
为矩形, ,
,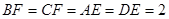 ,
,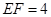 ,
, ,
,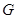 为
为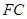 的中点,
的中点,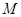 为线段
为线段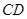 上的一点,且
上的一点,且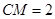 .
.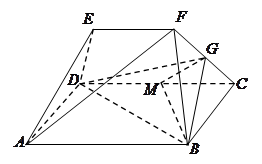
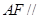 面
面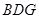 ;
;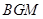
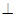 面
面 ;
; 的体积
的体积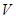 .
. ,底面
,底面 中
中 ,棱
,棱 ,
, 分别为
分别为 的中点.
的中点.
 >的值;
>的值;
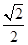 AB.
AB.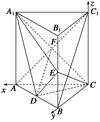





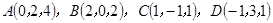 ,E,F分别是AB与CD的中点,则EF的长为( )
,E,F分别是AB与CD的中点,则EF的长为( )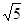
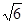
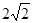
 共线,则
共线,则 =
=  =
=