Question

侧棱长为5cm，高为3cm的正棱锥的底面积为

3

3

．

Answer 1

分析：画出满足题意的三棱锥P-ABC图形，根据题意，作出高，利用直角三角形，求出此三棱锥的底面上的高及连长，即可求出棱锥的底面积．

解答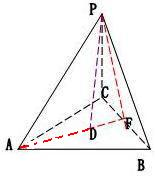：解：由题意作出图形如图：
因为三棱锥P-ABC是正三棱锥，F是BC的中点，顶点在底面上的射影D是底面的中心，
在三角形PDA中，
∵三角形PDA三边长PD=3，PA=5，
∴AD=

52-32

=4，
∴AF=

3

2

AD=

3

2

×4=6，BC=2BF=2×

3

3

AF=

3

则这个棱锥的底面积为S_底=

1

2

×BC×AF=

1

2

×

3

×6=3

3

．
故答案为：3

3

．

点评：本题考查棱锥的结构特征、棱锥的侧面积和表面积，还考查计算能力，是基础题．