题目内容
函数 的导函数为( )
的导函数为( )
A. | B.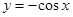 | C.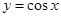 | D.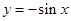 |
C
解析试题分析:因为 ,所以
,所以 。
。
考点:求导公式。
点评:直接考查求导公式,我们要把求导公式记熟,记准!属于基础题型。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线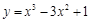 在点
在点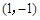 处的切线方程为
处的切线方程为
A.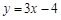 | B.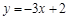 | C.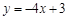 | D.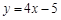 |
设函数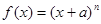 ,其中
,其中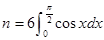 ,
, 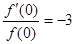 ,则
,则 的展开式中
的展开式中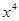 的系数为( )
的系数为( )
| A.-360 | B.360 | C.-60 | D.60 |
已知函数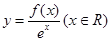 满足
满足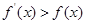 ,则
,则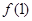 与
与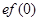 大小关系是( )
大小关系是( )
A.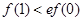 | B.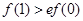 | C.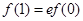 | D.不能确定 |
已知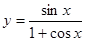 ,
,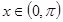 .当
.当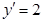 时,
时,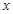 等于
等于
A.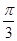 | B.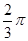 | C.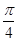 | D.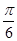 |
已知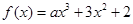 ,若
,若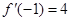 ,则
,则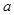 的值等于( )
的值等于( )
A.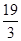 | B.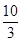 | C.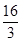 | D.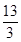 |
已知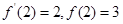 ,则
,则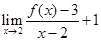 的值为 ( )
的值为 ( )
| A.1 | B.2 | C.3 | D.4 |
若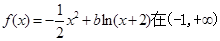 上是减函数,则
上是减函数,则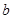 的取值范围是( )
的取值范围是( )
A. | B.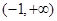 | C.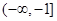 | D.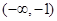 |
已知R上可导函数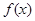 的图象如图所示,则不等式
的图象如图所示,则不等式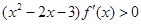 的解集为( )
的解集为( )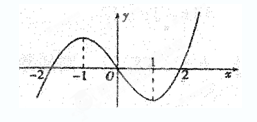
A. |
B.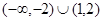 |
C.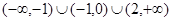 |
D.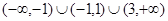 |