题目内容
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥底面ABCD, ![]() ,PA=2,E是PC上的一点,PE=2EC.
,PA=2,E是PC上的一点,PE=2EC.
(Ⅰ)证明:PC⊥平面BED;
(Ⅱ)设二面角A﹣PB﹣C为90°,求PD与平面PBC所成角的大小.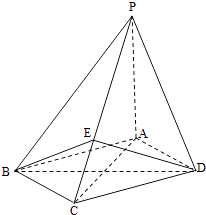
【答案】解:(I)以A为坐标原点,建立如图空间直角坐标系A﹣xyz,
设D( ![]() ,b,0),则C(2
,b,0),则C(2 ![]() ,0,0),P(0,0,2),E(
,0,0),P(0,0,2),E( ![]() ,0,
,0, ![]() ),B(
),B( ![]() ,﹣b,0)
,﹣b,0)
∴ ![]() =(2
=(2 ![]() ,0,﹣2),
,0,﹣2), ![]() =(
=( ![]() ,b,
,b, ![]() ),
), ![]() =(
=( ![]() ,﹣b,
,﹣b, ![]() )
)
∴ ![]()
![]() =
= ![]() ﹣
﹣ ![]() =0,
=0, ![]()
![]() =0
=0
∴PC⊥BE,PC⊥DE,BE∩DE=E
∴PC⊥平面BED
(II) ![]() =(0,0,2),
=(0,0,2), ![]() =(
=( ![]() ,﹣b,0)
,﹣b,0)
设平面PAB的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 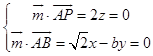
取 ![]() =(b,
=(b, ![]() ,0)
,0)
设平面PBC的法向量为 ![]() =(p,q,r),则
=(p,q,r),则 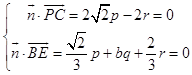
取 ![]() =(1,﹣
=(1,﹣ ![]() ,
, ![]() )
)
∵平面PAB⊥平面PBC,∴ ![]()
![]() =b﹣
=b﹣ ![]() =0.故b=
=0.故b= ![]()
∴ ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,2)
,2)
∴cos< ![]() ,
, ![]() >=
>= 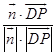 =
= ![]()
设PD与平面PBC所成角为θ,θ∈[0, ![]() ],则sinθ=
],则sinθ= ![]()
∴θ=30°
∴PD与平面PBC所成角的大小为30°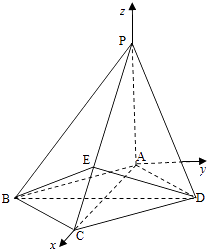
【解析】(I)先由已知建立空间直角坐标系,设D( ![]() ,b,0),从而写出相关点和相关向量的坐标,利用向量垂直的充要条件,证明PC⊥BE,PC⊥DE,从而利用线面垂直的判定定理证明结论即可;(II)先求平面PAB的法向量,再求平面PBC的法向量,利用两平面垂直的性质,即可求得b的值,最后利用空间向量夹角公式即可求得线面角的正弦值,进而求得线面角
,b,0),从而写出相关点和相关向量的坐标,利用向量垂直的充要条件,证明PC⊥BE,PC⊥DE,从而利用线面垂直的判定定理证明结论即可;(II)先求平面PAB的法向量,再求平面PBC的法向量,利用两平面垂直的性质,即可求得b的值,最后利用空间向量夹角公式即可求得线面角的正弦值,进而求得线面角
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想,以及对向量语言表述线面的垂直、平行关系的理解,了解要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若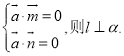 .
.

