题目内容
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC 平面ABC,
平面ABC, ,
,

(1)证明:平面ACD 平面ADE;
平面ADE;
(2)记 ,
, 表示三棱锥A-CBE的体积,求函数
表示三棱锥A-CBE的体积,求函数 的解析式及最大值
的解析式及最大值
(1)详见解析;(2)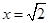 时,体积有最大值
时,体积有最大值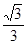
解析试题分析:(1)因为四边形DCBE为平行四边形,所以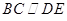 而易证
而易证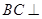 平面
平面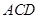 ,从而
,从而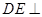 平面
平面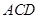 ,由面面垂直的判定定理可得,平面
,由面面垂直的判定定理可得,平面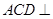 平面
平面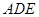 (2)三棱锥A-CBE的体积即为三棱锥E-ABC的体积,所以
(2)三棱锥A-CBE的体积即为三棱锥E-ABC的体积,所以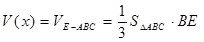
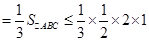 ,当OC
,当OC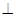 AB时取得最大值,此时
AB时取得最大值,此时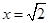
试题解析:(1)证明:因为四边形DCBE为平行四边形,所以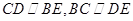
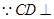 平面
平面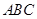 ,
,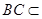 平面
平面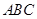 ,
,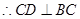
因为AB是圆O的直径,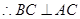 且
且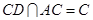
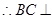 平面
平面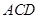 又
又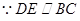 ,
,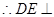 平面
平面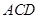
又 平面
平面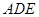 ,所以平面
,所以平面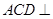 平面
平面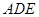 4分
4分
(2)∵ DC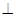 平面ABC ∴
平面ABC ∴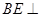 平面ABC
平面ABC
在Rt△ABE中,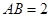 ,
,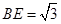
在Rt△ABC中 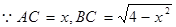 (
(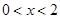 )
)
∴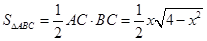 ,
,
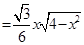 (
(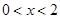 ) (8分)
) (8分)
备注:未指明定义域扣1分
∵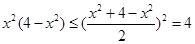 当且仅当
当且仅当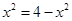 ,
,
即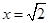 时,体积有最大值为
时,体积有最大值为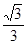 (12分)
(12分)
考点:1、空间直线与平面的位置关系;2、三棱锥的体积;3、最值问题

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
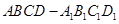 中,底面ABCD和侧面
中,底面ABCD和侧面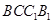 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,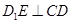 ,
,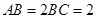 .
.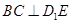 ;
;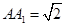 ,求三棱锥
,求三棱锥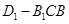 的体积.
的体积.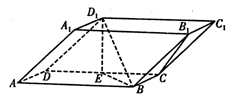
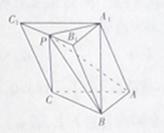
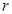 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?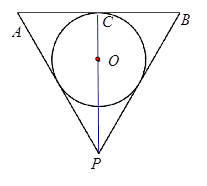
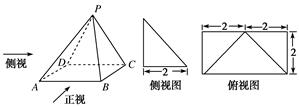
 ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.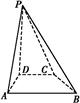
 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.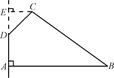
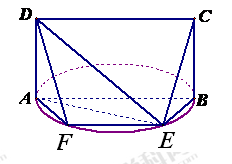
 与半圆弧的另一个交点为
与半圆弧的另一个交点为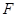
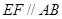
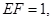 求三棱锥
求三棱锥 的体积
的体积