题目内容
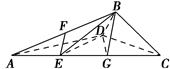
如图,E是以AB为直径的半圆上异于点A、B的点,矩形ABCD所在的平面垂直于该半圆所在的平面,且AB=2AD=2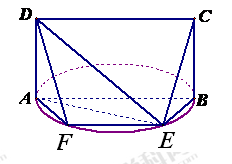
(1)求证: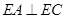
(2)设平面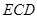 与半圆弧的另一个交点为
与半圆弧的另一个交点为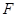
①试证: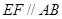
②若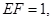 求三棱锥
求三棱锥 的体积
的体积
(1)详见解析;(2)①详见解析;②
解析试题分析:(1)证 面
面 得
得 。(2)①由
。(2)①由 可证得
可证得 平面
平面 ,根据线面平行的性质定理可得
,根据线面平行的性质定理可得 。②转化为以
。②转化为以 为顶点。
为顶点。
试题解析:解:(1)∵平面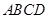
 平面
平面 ,
,
面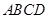
 面
面
 ,
, ,
, 面
面 ,
,
∴ 面
面 . 2分
. 2分
又∵ 面
面 ,
,
∴ . 3分
. 3分
∵ 在以
在以 为直径的半圆上,
为直径的半圆上,
∴ ,
,
又∵ ,
, 面
面 ,
,
∴ 面
面 . 4分
. 4分
又∵ 面
面 ,
,
∴ . 5分
. 5分
(2)① ∵ ,
, 面
面 ,
, 面
面 ,
,
∴ 平面
平面 . 6分
. 6分
又∵ 面
面 ,平面
,平面 平面
平面
 ,
,
∴ . 8分
. 8分
②取 中点
中点 ,
, 的中点
的中点 ,
,
在 中,
中, ,
, ,∴
,∴ .
.
(1)已证得 面
面 ,又已知
,又已知 ,
,
∴ 平面
平面 . 10分
. 10分
故
 . 12分
. 12分
考点:1线线垂直、线面垂直;2线线平行、平行;3棱锥的体积。

练习册系列答案
相关题目
 平面ABC,
平面ABC, ,
,

 ,
, 表示三棱锥A-CBE的体积,求函数
表示三棱锥A-CBE的体积,求函数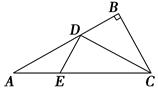
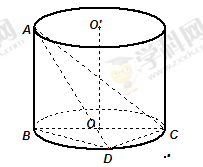
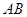 是圆柱体
是圆柱体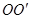 的一条母线,
的一条母线,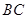 过底面圆的圆心
过底面圆的圆心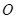 ,
,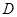 是圆
是圆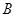 、
、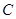 重合的任意一点,已知棱
重合的任意一点,已知棱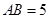 ,
,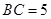 ,
,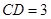 .
.
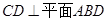 ;
;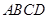 绕母线
绕母线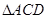 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.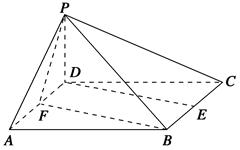
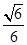 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.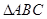 中,
中,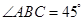 ,
,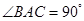 ,
,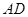 是
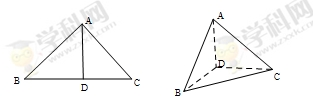
是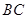 上的高,沿
上的高,沿 折起,使
折起,使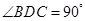 .
.
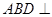 平面
平面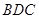 ;
;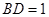 ,求三棱锥
,求三棱锥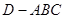 的体积.
的体积.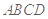 为矩形,
为矩形, 平面
平面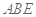 ,
,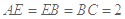 ,
,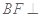 平面
平面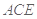 于点
于点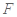 ,且点
,且点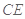 上.
上.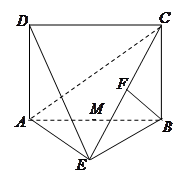
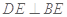 ;
;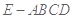 的体积;
的体积; 在线段
在线段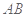 上,且
上,且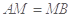 ,试在线段
,试在线段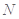 ,使得
,使得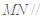 平面
平面 .
.