题目内容
若曲线y=g（x）在点（l，g（l））处的切线方程为y=2x+1，则曲线f（x）=g（x）+lnx在点（l，g（l））处切线的斜率为 ________，该切线方程为 ________．
3 y=3x
分析：先求出曲线y=g（x）的切点坐标，然后求出f'（x），从而求出切线的斜率，再求出曲线f（x）的切点坐标，即可求出切线方程．
解答：切线方程为y=2x+1过点（l，g（l））
∴g（l）=3，切点为（1，3），g'（x）=2
f'（x）=g'（x）+
∴f'（1）=g'（1）+1=3
f（1）=g（1）+ln1=3
∴切线方程为y=3x
故答案为：3，y=3x
点评：本题主要考查了利用导数研究曲线上某点切线方程，直线的斜率等有关基础知识，考查运算求解能力，考查转化思想，属于基础题．
分析：先求出曲线y=g（x）的切点坐标，然后求出f'（x），从而求出切线的斜率，再求出曲线f（x）的切点坐标，即可求出切线方程．
解答：切线方程为y=2x+1过点（l，g（l））
∴g（l）=3，切点为（1，3），g'（x）=2
f'（x）=g'（x）+
∴f'（1）=g'（1）+1=3
f（1）=g（1）+ln1=3
∴切线方程为y=3x
故答案为：3，y=3x
点评：本题主要考查了利用导数研究曲线上某点切线方程，直线的斜率等有关基础知识，考查运算求解能力，考查转化思想，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
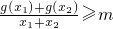恒成立，求实数m的最大值．