Question

若实数x、y满足约束条件

x-4y+3≤0 3x+5y-25≤0 x≥1

，目标函数z=kx+y的最大值为12，最小值为3，则实数k的值为（　　）

• A、1
• B、2
• C、3
• D、4

Answer 1

考点：简单线性规划的应用

专题：数形结合,不等式的解法及应用

分析：由约束条件作出可行域，然后分k=0，k＜0和k＞0三种情况讨论使目标函数取得最值时的最优解，联立方程组后求解k的值．

解答： 解：由约束条件

x-4y+3≤0 3x+5y-25≤0 x≥1

，作出可行域如图，

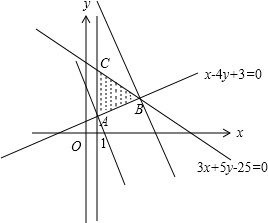
可行域为△ABC的边界及其内部，求解直线交点得：A（1，1），B（5，2），C（1，

22

5

）．
由目标函数z=kx+y，得y=-kx+z，
若k=0，目标函数z=kx+y取得最大值时的最优解为C（1，

22

5

），最大值为

22

5

，不合题意；
若k＜0，则-k＞0，目标函数z=kx+y取得最大值时的最优解为C（1，

22

5

），
当0＜-k≤

1

4

，即-

1

4

≤k＜0时，目标函数z=kx+y取得最小值时的最优解为A（1，1），
联立

12=k+ 22 5 3=k+1

，k无解，
当-k＞

1

4

，即k＜-

1

4

时，目标函数z=kx+y取得最小值时的最优解为B（5，2），
联立

12=k+ 22 5 3=5k+2

，k无解．
若k＞0，则-k＜0，目标函数z=kx+y取得最小值时的最优解为A（1，1），
若-

3

5

≤-k＜0，即0＜k≤

3

5

时，目标函数z=kx+y取得最大值时的最优解为C（1，

22

5

），
联立

3=k+1 12=k+ 12 5

，k无解．
若-k＜-

3

5

，即k＞

3

5

时，目标函数z=kx+y取得最大值时的最优解为B（5，2），
联立

3=k+1 12=5k+2

，解得k=2．
综上，使目标函数z=kx+y的最大值为12，最小值为3的实数k的值为2．
故选：B．

点评：本题考查了简单线性规划的应用，考查了数形结合的解题思想方法与分类讨论的数学思想方法，是中档题．