题目内容
已知
的顶点A（0，1），AB边上的中线CD所在直线方程为
，AC边上的高BH所在直线方程为
.
（1）求的项点B、C的坐标
（2）若圆M经过不同的三点A、B、P（m、0），且斜率为1的直线与圆M相切于点P
求：圆M的方程
解（1）AC边上的高BH所在直线方程为y=0,所以AC: x=0
又CD: ，所以C(0, 
) …………………………2分
设B(b, 0)，则AB的中点D(
)，代入方程
解得b=2, 所以B(2, 0) ……………………………………………………4分
（2）由A(0, 1), B(2, 0)可得，圆M的弦AB的中垂线方程为
BP也是圆M的弦，所以圆心在直线
上. 设圆心M
因为圆心M在直线上，所以
①
又因为斜率为1的直线与圆M相切于点P，所以
.
即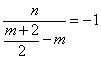
，整理得：
②
由①②可得：
，所以
，半径
所以所求圆的方程为
练习册系列答案
优学名师名题系列答案
相关题目