题目内容
中心在原点的椭圆E:
+
=1(a>b>0)的一个焦点为圆C:x2+y2-4x+2=0的圆心,离心率为
.
(1)求椭圆E的方程;
(2)椭圆E上是否存在一点P,使得过P点的两条斜率之积为
的两条直线l1、l2,与圆C相切?若存在,求出点P的坐标,若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆E的方程;
(2)椭圆E上是否存在一点P,使得过P点的两条斜率之积为
| 1 |
| 2 |
分析:(1)确定x2+y2-4x+2=0的圆心C(2,0),可得c=2,利用离心率为
,即可求得椭圆E的方程;
(2)设P(x0,y0),l1,l2的斜率分别为k1,k2,则k1k2=
,由l1与圆C:x2+y2-4x+2=0相切,可得k1,k2是方程[(2-x0)2-2]k2+2(2-x0)y0k+y02-2=0的两个实根,结合P在椭圆上,即可求得结论.
| 1 |
| 2 |
(2)设P(x0,y0),l1,l2的斜率分别为k1,k2,则k1k2=
| 1 |
| 2 |
解答:解:(1)由x2+y2-4x+2=0得(x-2)2+y2=2,∴圆心C(2,0)
∵椭圆的一个焦点为圆C:x2+y2-4x+2=0的圆心,离心率为
.
∴c=2,
=
,∴a=4,
∴b2=a2-c2=12
∴椭圆E的方程为
+
=1;
(2)设P(x0,y0),l1,l2的斜率分别为k1,k2,则l1:y-y0=k1(x-x0),l2:y-y0=k2(x-x0),且k1k2=
由l1与圆C:x2+y2-4x+2=0相切得
=
∴[(2-x0)2-2]k12+2(2-x0)y0k1+y02-2=0
同理可得[(2-x0)2-2]k22+2(2-x0)y0k2+y02-2=0
从而k1,k2是方程[(2-x0)2-2]k2+2(2-x0)y0k+y02-2=0的两个实根
所以
①,且k1k2=
=
∵
+
=1,
∴5x02-8x0-36=0,
∴x0=-2或x0=
由x0=-2得y0=±3;由x0=
得y0=±
满足①
故点P的坐标为(-2,3)或(-2,-3),或(
,
)或(
,-
)
∵椭圆的一个焦点为圆C:x2+y2-4x+2=0的圆心,离心率为
| 1 |
| 2 |
∴c=2,
| c |
| a |
| 1 |
| 2 |
∴b2=a2-c2=12
∴椭圆E的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)设P(x0,y0),l1,l2的斜率分别为k1,k2,则l1:y-y0=k1(x-x0),l2:y-y0=k2(x-x0),且k1k2=
| 1 |
| 2 |
由l1与圆C:x2+y2-4x+2=0相切得
| |2k1+y0-k1x0| | ||
|
| 2 |
∴[(2-x0)2-2]k12+2(2-x0)y0k1+y02-2=0
同理可得[(2-x0)2-2]k22+2(2-x0)y0k2+y02-2=0
从而k1,k2是方程[(2-x0)2-2]k2+2(2-x0)y0k+y02-2=0的两个实根
所以
|
| y02-2 |
| (2-x0)2-2 |
| 1 |
| 2 |
∵
| x02 |
| 16 |
| y02 |
| 12 |
∴5x02-8x0-36=0,
∴x0=-2或x0=
| 18 |
| 5 |
由x0=-2得y0=±3;由x0=
| 18 |
| 5 |
| ||
| 5 |
故点P的坐标为(-2,3)或(-2,-3),或(
| 18 |
| 5 |
| ||
| 5 |
| 18 |
| 5 |
| ||
| 5 |
点评:本题考查椭圆的标准方程,考查直线与圆相切,解题的关键是确定k1,k2是方程[(2-x0)2-2]k2+2(2-x0)y0k+y02-2=0的两个实根.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
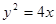 以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为
▲ .
以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为
▲ .  (a>b>0)的一个焦点为圆C:x2+y2-4x+2=0的圆心,离心率为
(a>b>0)的一个焦点为圆C:x2+y2-4x+2=0的圆心,离心率为 .
. ,与圆C相切?若存在,求出点P的坐标,若不存在,请说明理由.
,与圆C相切?若存在,求出点P的坐标,若不存在,请说明理由.