题目内容
17. 已知正四棱柱ABCD-A1B
(1)证明EF为BD1与CC1的公垂线;
(2)求点D1到面BDE的距离.

17.

(Ⅰ)证明:取BD中点M,连结MC、FM,
∵F为BD1中点,
∴FM∥D1D且FM=![]() D1D.
D1D.
又EC=![]() CC1且EC⊥MC,
CC1且EC⊥MC,
∴四边形EFMC是矩形,
∴EF⊥CC1.
又CM⊥面DBD1,
∴EF⊥面DBD1,
∵BD1![]() 面DBD1,
面DBD1,
∴EF⊥BD1.
故EF为BD1与CC1的公垂线.
(Ⅱ)解:连结ED1,有![]()
由(Ⅰ)知EF⊥面DBD1,
设点D1到面BDE的距离为d,
则S△DBE·d=![]() ·EF.
·EF.
∵AA1=2,AB=1,
∴BD=BE=ED=![]() ,EF=
,EF=![]() .
.
∴![]() =
=![]() ·
·![]() ·2=
·2=![]() ,
,
S△DBE=![]() ·
·![]() ·(
·(![]() )2=
)2=![]() .
.
∴d=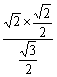 =
=![]() .
.
故点D1到平面BDE的距离为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.
(文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.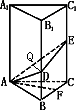
 的底边AB=2cm,D、E分别是侧棱
的底边AB=2cm,D、E分别是侧棱 B、
B、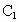 C上的点,且有EC=BC=2DB.
C上的点,且有EC=BC=2DB.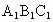 的底边AB=2cm,D、E分别是侧棱
的底边AB=2cm,D、E分别是侧棱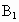 B、
B、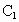 C上的点,且有EC=BC=2DB.
C上的点,且有EC=BC=2DB.
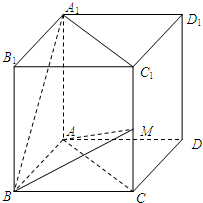 (文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.
(文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上. ,求多面体ABM-A1B1C1的体积.
,求多面体ABM-A1B1C1的体积.