题目内容
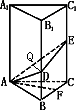
如图,已知正三棱柱A1B1C1-ABC的底面积等于![]() cm2,D、E分别是侧棱B1B,C1C上的点,且有EC=BC=2DB,试求
cm2,D、E分别是侧棱B1B,C1C上的点,且有EC=BC=2DB,试求
(1)四棱锥A-BCDE的底面BCED的面积
(2)四棱锥A-BCED的体积
(3)截面ADE与底面ABC所成二面角的大小
(4)截面ADE的面积
答案:
解析:
提示:
解析:
|
答:(1)SBCED=3 cm2,(2)VA-BCED= 解:设ΔABC边长为x,∵SΔABC= ∴AF⊥平面BCED,VA-BCED= 在RtΔABD中,AD2=AB2+DB2=22+12=5;在Rt梯形BCED中,DE2=(CE-DB)2+BC2=5 ∴AD=DE= 在RtΔACE中,AE2=EC2+AC2=8,DQ2=AD2-AQ2=( ∴AE= 设截面ADE与底面ABC所成二面角大小为α,D、E分别在底面的射影为B、C,∴ΔABC的面积=ΔADE面积×cosα 即 |
提示:
|
利用三棱柱的性质及已知条件,(1)、(2)、(4)不难推算,至于(3),可设平面ADE与平面ABC所成二面角为α,观察到ΔADE在底面ABC的射影是ΔABC(∵DB⊥平面ABC,EC⊥平面ABC)应用SΔABC=SΔADE·cosα,可求出α. |

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点, (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为