题目内容
已知正三棱柱ABC-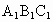
的底边AB=2cm，D、E分别是侧棱
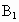B、
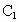C上的点，且有EC=BC=2DB．
求四棱锥A-BCED的体积．
答案：略
解析：
解析：
|
解：正三棱 ABC- 中B ⊥底面ABC，C ⊥底面ABC，且BC 平面ABC，
∴ B⊥BC，C⊥BC，则DB∥EC，且∠DBC=90°，
∴四边形 BCED是直角梯形．由于 EC=2DB=BC=2，∴DB=1．
取 BC的中点F，连结AF，则AF⊥BC由于平面ABC⊥平面BC ，
由两个平面垂直的性质定理，有 AF⊥平面 ，
即 AF为四棱锥A-BCED的高，且AF= AB= ．
∴  ．
如图所示，要计算四棱锥 A-BCED的体积，一是应计算好四边形BCED的面积，二是应计算好这个四棱锥的高． |
(cm)
练习册系列答案
全能测控期末小状元系列答案
相关题目
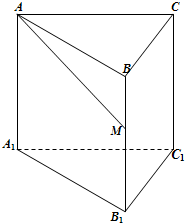如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞2），动点M在侧棱BB1上移动．设AM与侧面BB1C1C所成的角为θ．
已知正三棱柱ABC-A1B1C1的每条棱长均为a，M为棱A1C1上的动点．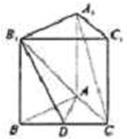
如图，已知正三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=1．
（2009•湖北模拟）如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为棱A1B上的动点．